Calculate Equivalent Resistance & Current Thru R1: Ohm's Law Problem

In summary, the equivalent resistance of the network is 17.86 ohm. To find the current through R1, the voltage drop across R4 must first be calculated. This is because the voltage across R1 and R4 together equals the total voltage. The direction of the current does not affect the calculations.
  • #1
mujadeo
103
0

Homework Statement


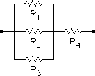
Calculate the equivalent resistance of the network shown in the diagram. The resistances are: R1 = 12 ohm, R2 = 5 ohm, R3 = 15 ohm, and R4 = 15 ohm.

no prob here

Req = [(1/12)+(1/5)+(1/15)]^-1 + 15 = 17.86ohm

When a battery with E = 6 V and zero internal resistance is attached across this network, what current flows through resistor R1?



Homework Equations


Cant figure out if the current thru R1 is actually Req or R1.
When i use V=IR none of the answers come out correct.
Please help


The Attempt at a Solution

 

Attachments

  • showme.gif
    showme.gif
    631 bytes · Views: 443
Physics news on Phys.org
  • #2
To find the current through R1, find the voltage across it. Hint: First find the voltage drop across R4.
 
  • #3
why do i need to know voltage drop across r4?
also does it matter which dorection the current is going?
 
  • #4
mujadeo said:
why do i need to know voltage drop across r4?
Because the voltage across R1 + the voltage across R4 adds up to the total voltage.
also does it matter which dorection the current is going?
No, that just depends on which way the battery was connected.
 
  • #5
ok i needed to relearn circuit breakdown and then build it back up.
thanks
 

FAQ: Calculate Equivalent Resistance & Current Thru R1: Ohm's Law Problem

1. What is Ohm's Law?

Ohm's Law is a fundamental principle in physics that describes the relationship between voltage, current, and resistance. It states that the current through a conductor is directly proportional to the voltage applied across it, and inversely proportional to the resistance of the conductor.

2. How do you calculate equivalent resistance?

To calculate equivalent resistance, you must first determine the resistances of all the components in the circuit. Then, use Ohm's Law (R = V/I) to calculate the resistance for each individual component. Finally, add all the individual resistances together to get the total equivalent resistance.

3. How do you calculate current through a specific resistor?

To calculate current through a specific resistor, you can use Ohm's Law (I = V/R) where I is current, V is voltage, and R is resistance. Plug in the values for the voltage and the resistance of the specific resistor, and you will get the current through that resistor.

4. What is the unit of resistance?

The unit of resistance is ohms (Ω). It is named after the German physicist Georg Ohm, who first stated the relationship between voltage, current, and resistance in 1827.

5. Can you use Ohm's Law to calculate the resistance of a non-ohmic material?

No, Ohm's Law only applies to ohmic materials, which have a constant resistance regardless of the voltage applied. Non-ohmic materials have a varying resistance, so Ohm's Law cannot be used to calculate their resistance.

Similar threads

Ohm's Law - Finding Source Voltage
Replies
3
Views
998
Total equivalent resistance of a combined circuit
Replies
7
Views
2K
Calculate the equivalent resistance
Replies
11
Views
2K
How to solve this chain with Kirchhoff's laws?
Replies
18
Views
2K
Voltage, Current, and Resistance Calculations
Replies
13
Views
1K
Ohm's law and Kirchoff — What am I missing?
Replies
4
Views
1K
The equivalent resistance for the resistors in this circuit?
Replies
5
Views
2K
Electric current and resistance question
Replies
2
Views
1K
Parallel circuit with internal resistance
Replies
6
Views
1K
How to make total resistance of 1 ohm?
Replies
7
Views
1K

Hot Threads

Recent Insights

Back
Top