Ohm's law and Kirchoff — What am I missing?

[vlady66]

[Moved to homework, so no template]

Summary:: trying to figure out physics for current and having issues. keep getting something that does not make sense.

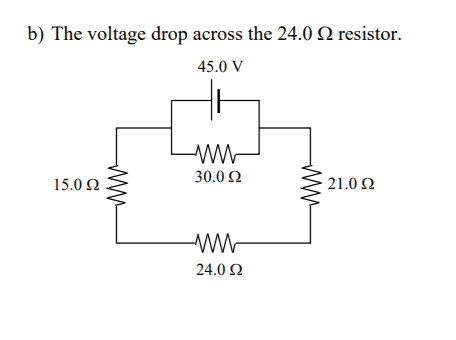
working on this issue, and i think i have to find ttl resistance, to find current using ohms law. looking at the circuit attached there is two loops. Regardless my understanding is the voltage in each circuit should equal 45v. I have gotten current from 1.5, 1.8, 2.2 Amps but when applying ohms law for each voltage drop at each resistor the total voltage exceeds 45v and it should not. I am missing something here...what is the voltage drop across 24Ω . now it cannot be as simple as I=45/24...I tried the Rtotal r1=21 and clock wise. So R4 30Ω i got 1.5 A, but to find Rt it is 21+24+15=60Ω
then i tried the I=(1/r+1/Rs)^-1... so i got (1/30 + 1/60)^-1= 0.046 then invert 21.7 is my ttl Resistance. This is kinda where i go sideways...Ohms law v=IR so this converts to I=v/r which is I=45/21.7= 2.07A... but that does not seem right as voltage drop at 24Ω is v=2.07(24)=50v which is wrong, it can not exceed 45V, what am i doing wrong. Please advise...frustrated...grrrrrr

 

[Nugatory]

Ask yourself: what is the current through that 24 ohm resistor? The rule about resistors in series will be helpful

 

[berkeman]

looking at the circuit attached there is two loops. Regardless my understanding is the voltage in each circuit should equal 45v.

Correct, that is the key.

The voltage source is putting 45V across the 30 Ohm resistor, and it is also putting 45V across the series combination of the other 3 resistors. Work out the current through each of those two loops independently, since they are in parallel. It is the voltage source's job to source enough current to be able to hold that 45V across those two parallel strings of resistors.

Finding the current through the 30 Ohm resistor with the 45V across it is easy, right? Then find the current in the other loop that is going through the series combination of those 3 resistors, and then you can figure out the individual voltage drops across each of the three resistors because you know the current through them.

Show us those calcs so we can be sure you are understanding things now.

 

[vlady66]

i think i figured it out but maybe I am over thinking this. as seen below i split them into two distinct circuits. to answer the question the voltage drop would be 18v, if the current calculation is 0.75Ω. Not sure why i struggled with this, i am mixing things up..

 

[vela]

Part of your confusion might be caused by not knowing how to do calculations accurately. For example, when you calculated the total combined resistance, it looks like you did something like this:
$$\frac{1}{30.0} + \frac{1}{60.0} = 0.03 + 0.016 = 0.046.$$ If you had kept more digits on the intermediate steps and rounded correctly, it would have helped a lot:
$$\frac{1}{30.0} + \frac{1}{60.0} = 0.03333 + 0.01667 = 0.0500.$$ The excessive truncating on intermediate steps led to a result that wasn't very accurate. Generally, I'd suggest keeping one extra sig fig on intermediate results if you're going to insist on truncating them. Personally, I just keep all the digits on the calculator until the end and then round to the correct number of sig figs. Better yet, you could have done the calculation pretty easily by hand:
$$\frac{1}{30} + \frac{1}{60} = \frac{2 + 1}{60} = \frac{1}{20} = 0.05.$$ The correct resistance is 20.0 ohms, not 21.7 ohms.

With the inaccurate resistance, you found a current of 2.07 A. It's not apparent how this figure is related to the currents you found for the individual loops. But with the equivalent resistance of 20 ohms, you get 2.25 A, which is apparently the sum of the individual currents. If you understand why this should be the case, it's hopefully clear why taking this current and multiplying it by 24.0 ohms isn't the right way to find the voltage across that resistor.