Calculate Normal Forces for Particle P in Vertical Slot - Homework Problem

[drawar]

Homework Statement

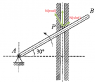
Particle P has a mass of 1kg and is confined to move along the smooth vertical slot due to the rotation of the arm Ab. Assume that at the instant as shown, the acceleration of the particle P is 2.46 m/s^2 upward. Determine the normal force N(rod) on the particle by the rod and the normal force N(slot) on the particle by the slot in the position shown. Frictions forces are negligible.

----N(rod) ---- N(slot)
A. 14.2 N ---- 7.1 N
B. 10.5 N ---- 3.6 N
C. 7.1 N ---- 14.2 N
D. 3.2 N ---- 1.6 N

Homework Equations

F= ma

The Attempt at a Solution

F = ma = 2.46 N
The force acting on the particle can be resolved into 2 components
N(rod) = F x cos(30) = 2.13 N
N(slot) = F x sin(30) = 1.23 N

The answer does not match any of the choices provided. Can someone help me figure out what I'm doing wrong? Thanks

 

[cupid.callin]

Hi drawar
Welcome to PF!


a diagram would be nice.

 

[drawar]

Hi cupid.callin :)
I've already drawn a vector diagram showing my work

 

[RTW69]

Your N(slot) force is in the wrong direction. N(rod) is correct. If you resolve N(rod) onto forces in the x and y directions you will see that N(slot) must act in the positive x-direction (to the right). Draw a free body diagram with all forces. Identify direction of acceleration. Use F=ma for x and y directions.

 

[darkxponent]

let AP= l
and vertical position of particle = y
now: y= l*sine(theeta)


velocity of particle= v= dy/dt= l*cos(theeta)*d(theeta)/dt
v = Vr*cos(theeta)

acc of paticle = a= dv/dt = (-)*l* sine(theeta) *w + l*cos(theeta)* q {q=angular acc of rad, w= angular vel of rad}

acc of particle = -Vr*sin(theeta) + Ar*cos(theeta)

{Vr , Ar = velocity of rod, Accc of rod at particles point}

this means :: DATA insufficient...either posotion or velocity particle is required

 

[gneill]

The answer does not match any of the choices provided. Can someone help me figure out what I'm doing wrong? Thanks

How is the gravitational force being accounted for (the particle has a mass, therefore a weight)? I don't see it in your FBD or calculations.

 

[cupid.callin]

Am i the only one who still can't see the pic?

 

[drawar]

Thanks for all your kind help :-)
I totally forgot about the gravitational force. I've just give it another try and here is the result, hope someone might have a check at this:

Resolving vertically upward:
$$N_{rod} \times \cos 30^o - mg = ma \Rightarrow N_{rod} = \frac{{m(g + a)}}{{\cos 30^o }} = 14.2$$(1 d.p)

Resolving horizontally rightward:
$$N_{slot} - N_{rod} \times \sin 30^o = 0 \Rightarrow N_{slot} = \frac{{N_{rod} }}{{\sin 30^o }} = 7.1$$

Hence choose A

edit: @cupid.callin: I'm afraid so. Seems like your browser is having trouble reading image from imgur.com. I'll upload it to another host