Calculate Output Voltage of Op-Amp Circuit

[Number2Pencil]

Homework Statement

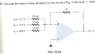
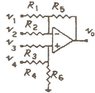
Find the output voltage. a picture is attached giving all information.

The Attempt at a Solution

I'm new to op-amps, and I wasn't sure how to go about solving this. I thought it looked like an inverting op-amp but I wasn't sure. Since I wasn't sure, I tried to use superposition on V1, V2, and V3 to get the Vout. When I did this (my work is attached), I started with V1 and grounded out V2 and V3. I still wasn't sure on what to do from there so I tried to make an equivalent circuit to help but it ended up confusing me more as it looked like Vout = 0V.

I need some pointers, and if someone could give me a "plan" on what to do if I get a problem like this where I'm not sure what type of op-amp it is, I'd appreciate it.

 

[berkeman]

You solution isn't correct yet. When working with opamps, you usually use the ideal opamp assumptions, which are infinite input impedance (so no current goes in or out of the + and - terminals), and infinite gain (so the - input is held at the same voltage as the + input via the output voltage fed back to the - input).

In this problem, you should just write a KCL equation at the - input terminal. Call the voltage there Vn, and write the equation that shows that the sum of all currents leaving that node is zero. That will give you the solution.

 

[Number2Pencil]

alright berkeman, here is me trying to do what you suggested. My answer ended up being -31.5V

I'm not sure if I used the right signs (+ or -) in my equation, or if I'm even doing what you said. lol

 

[Number2Pencil]

here's a noob question for you:

if the + and - inputs were switched, would it make a difference? I wonder because on the ideal they seem to be treated the same way

The reason I ask is because the book gives a pretty nice formula for summing op-amps (hence I wouldn't have to redraw an equivalent circuit and confuse myself), but the only thing is in every example the book shows, the + and - on the op amp are switched, So I was wondering if I can treat this problem the same way. It would make it easier, even though I still want to know how to solve a "crazy" looking one

 

[Gokul43201]

I wonder if there isn't an error in the diagram, and they accidentally switched the inputs. Where does this question come from?

 

[berkeman]

I wonder if there isn't an error in the diagram, and they accidentally switched the inputs. Where does this question come from?

Oops, you're right! That's either a typo or a trick question. Sorry that I didn't notice it when I first looked at it -- I always draw my opamps with the inverting input on top, so I totally missed that.

Pencil, the reason that you use negative feedback is to stabilize the transfer function to whatever linear function you are trying to acheive. The only time you use positive feedback (that I know of) is for hysteresis and switching applications.

 

[berkeman]

alright berkeman, here is me trying to do what you suggested. My answer ended up being -31.5V

I'm not sure if I used the right signs (+ or -) in my equation, or if I'm even doing what you said. lol

No, if the +/- inputs were switched like a normal opamp circuit, I get an answer between 1V and 2V. With the inputs backwards like that, the opamp will peg its output at one of the power supply rails. Think about what happens with small variations at the + input. Say the + input starts out exactly at 0V like the - input shown... Let's say a little noise or something makes the + input slightly above 0V. That will push the output higher in voltage by the gain of the opamp multiplied by the slightly positive voltage at the + input. But that will push the + input up more, which pushes the output up more, and boom, the output rails out at the positive supply voltage. Positive feedback creates an instability that results in the output pegging at one rail or the other.

So the answer to the literal circuit the way it was presented is that the output rails out positive or negative. Quiz question -- what answer do you get if you swap the +/- input symbols to make it a more conventional opamp circuit?

 

[Number2Pencil]

To Gokul: Boylestad/Nashelsky's Electronic Devices and Circuit Theory 9th ed.
If you're saying it's a typo i'd believe it because this is from my first homework assignment.

Quiz question -- what answer do you get if you swap the +/- input symbols to make it a more conventional opamp circuit?

Well that's a bit easier because I can use a formula straight from the book:

Vo = -[V1(Rf/R1) + V2(Rf/R2) + V3(Rf/R3)]

which gives me: -16.5V.

But I know that not every one of these is going to have a nice formula for me to remember. In fact I have a big sheet of some crazy looking op-amps I have to reduce to a single equation with only Vo as the unknown. So I'm going to have to get pro at this pretty soon.

 

[Number2Pencil]

hmm...I think I actually might of achevied getting that equation on my own:

I assumed all currents from V1, V2, and V3 were going into the node Vn (which is zero volts), and all that current was exiting through the Rf branch (by Kirchoff's Current Law & the fact that no current can go into the op-amp terminals). This gave me:

KCL: V1/R1 + V2/R2 + V3/R3 = Vo/Rf

Solving for Vo:

Rf(V1/R1 + V2/R2 + V3/R3) which gives me 16.5V which is right except for the SIGN. But both of those might be wrong since Berkeman said it was between 1V and 2V.

 

[berkeman]

To Gokul: Boylestad/Nashelsky's Electronic Devices and Circuit Theory 9th ed.
If you're saying it's a typo i'd believe it because this is from my first homework assignment.



Well that's a bit easier because I can use a formula straight from the book:

Vo = -[V1(Rf/R1) + V2(Rf/R2) + V3(Rf/R3)]

which gives me: -16.5V.

But I know that not every one of these is going to have a nice formula for me to remember. In fact I have a big sheet of some crazy looking op-amps I have to reduce to a single equation with only Vo as the unknown. So I'm going to have to get pro at this pretty soon.

Ah, I see why I got -1.65V... I misread the feedback resistor as 33k, not 330k.

Quiz question -- why is -16.5V not really a good answer in practical terms?

And as for memorizing formulas, don't bother with most opamp circuits. The results are easy to derive for most opamp circuits as long as you just visualize the simplifying assumptions of the ideal opamp.


EDIT -- I should have had a negative sign in front of both my 1.65V and 16.5V numbers in this post. I've corrected them here, and will post a note below.

 

[berkeman]

KCL: V1/R1 + V2/R2 + V3/R3 = Vo/Rf

Solving for Vo:

Rf(V1/R1 + V2/R2 + V3/R3) which gives me 16.5V which is right except for the SIGN. But both of those might be wrong since Berkeman said it was between 1V and 2V.

You are correct with an answer of -16.5V when the opamp +/- inputs are corrected (well, except for my last quiz question point). The sign has to be negative because there is a net current going from left to right through the feedback resistor, which means that Vo will be below ground. The reason the sign isn't right in your equations above is that you equated the currents into the node from the left with the current into the node from the right. You should have equated the currents into the node from the left with the currents *out* of the node to the right. Or just used the more traditional KCL where you write the total sum of all currents out of a node and set that equal to zero and solve.

So you're pretty much done, except for that last (optional but still important) quiz question. Why is it generally not practical in simple opamp circuits to have an output voltage of -16.5V?

 

[Number2Pencil]

i'm sorry berkeman...I really don't know the final question

ok I'll take a stab for maybe partial credit. I'll guess that it...uses too much power!

::lowers head in shame::

 

[Gokul43201]

ok I'll take a stab for maybe partial credit. I'll guess that it...uses too much power!

Here's a hint: Is an op-amp a passive device or an active device?

 

[Number2Pencil]

alright, time for guess #2/3/4/5.

Yes it's active, I found out they require a power source. As for not being practical...well you started out with a few small voltages and ended up with negative 16.5 Volts, so you've at least amplified something. As for applying this -16.5 volts, well if you connect a resistor to that and to ground, you'd get a current flowing TOWARDs the op-amp terminal...but it already has a current going the opposite way, so that'd probably explode. I guess that's not what you'd do with it...I don't think many things run off of -16.5 Volts either. You could connect that to another op-amp but that's not what the question is asking. I guess you could attach a 16.5V Voltage source (if they exist) to the terminal and ground...but then you'd have a big circle of amplifying to a negative voltage and raising the voltage back to ground...seems kinda useless
::lowers head again::

okay, I'm done embarassing myself. if it has something to do with the practical op-amp model, I haven't learned about it yet. But you can give me the answer now!

 

[berkeman]

No worries, that's what extra credit quiz questions are for -- to learn a little bit extra. As Gokul hinted, the opamp is an active device which requires a power supply. You will generally run opamps either from a single supply (5V or 12V and ground) or from symmetric split supplies (like +/- 12V). And opamps have varying capability to drive their output signals near the rails -- typical opamps can only drive their output to within a volt or so of their power supply rails. (And there are limits to how close the inputs can come to the power supply rails as well.)

So for a practical opamp (which still comes close to ideal in terms of very high input impedance and high gain, BTW) that is running off of a typical +/- 12V power supply, there is no way that it can drive its output to -16.5V. Most likely the output would peg at around -11V or so.

BTW, I'd recommend that you check out the textbook "The Art of Electronics" by Horowitz and Hill, as a good side-reference text while you learn the basics of opamps and electronics. One of the features of that book is a section at the end of each chapter called something like "Bad Circuits", where it shows common errors that people make in basic electronic circuits. Trying to have an output voltage of -16.5V out of an opamp that has +/- 12V power supply rails would be a typical thing that would get shown in that section.

 

[Number2Pencil]

hmm..I did not know that. Thanks. I thought op-amps were the magical triangles of electronics that give you whatever you want whenever you want it. I know now that this is not so and these homework problems are for practice not application. I have much more to learn on my journey to the design stage.

Thanks Berkeman, you deserve money for all the free help you give me. Thanks to you to Gokul

 

[Number2Pencil]

alright this is the last one i swear! What would be the easiest way to go about solving the attached problem in terms of Vo?

here was my plan:

1) Label the points next to both terminals as Vx.
2) Solve for Vx in terms of V3,V4,R3,R4, & R6 using nodal analysis.
3) Solve for Vo using KCL at the point Vx on the negative terminal in terms of V1, V2, R1, R2, Vx, and R5.
4) plug equation from part 2 into equation from part 3.


I'm getting some ugly looking equations for these final problems on this worksheet. Am I missing a helpful trick or are these types just going to get messy? Is there even a way to tell if I got it right?

 

[berkeman]

Sounds like a plan to me!

 

[Number2Pencil]

if anyone feels like checking my answer I got

<br /> V_O = -R_5 (\frac{V_1 - \frac{V_3 R_4 R_6 + V_4 R_3 R_6}{R_6 R_4 + R_6 R_3+ R_3 R_4}}{R_1} + \frac{V2 - \frac{V_3 R_4 R_6 + V_4 R_3 R_6}{R_6 R_4 + R_6 R_3 + R_3 R_4}}{R_2})<br />

that's not pretty, but neither am I

I actually ended up using the "Summing Amplifier" equation from the book after I found Vx (yeah I cheated)

 

[teknodude]

Nothing wrong with Summing Amplifier equation. I would have used it too, just because of laziness.

Well if you want to check it, go back and do it using nodal analysis and see if you get the same answer.

 

[doodle]

Hmm... a preliminary check reveals that there are some missing terms in the expression. I would suggest the more straightforward approach of using superposition to obtain the final answer, i.e., to consider each input (V1 to V4) in turn and to sum up the (output) response of these independent inputs.
As a hint, output V0 with only V1 activated gives V0 = -(R5/R1) V1. In the same token, considering only the input V2, we get V0 = -(R5/R2) V2. Try to obtain V0 for the other two inputs.

 

[Number2Pencil]

I'm doing it doodle's way (seems a ton easier). but I need some help again. I'm finding V3 now by grounding the other sources, and it looks almost like a non-inverting op-amp set up. So I know I can just borrow the formula I already obtained from another problem:

<br /> V_O = V_N (1 + \frac{R_F}{R_N})<br />

I know RF = R5 and RN = R3, but what should I use for the voltage being amplified? I want to say it's the voltage right beside the + terminal, which would be a voltage divider (i usually label it Vx):

<br /> V_X = V_3 ( \frac{R_4//R_6}{R_3 + R_4//R_6} <br />

then plug that in for Vn. Is this correct?

 

[doodle]

The second equation looks correct; in the first equation, RF = R5 is right, but RN = R3 is not. You're getting close. :)

 

[Number2Pencil]

I got it!

Rn = R1//R2

 

[doodle]

Yup, that's the answer alright. Well done! :)

 

[Number2Pencil]

woo hoo! well I guess I can do the next problem now. ::brain melts::

 

[Number2Pencil]

here's a new one giving me trouble: Find an equation for I_L in terms of V_I R & R_L. there's an additional problem asking what I_L is when R_L is different numbers.

I started with a KVL around the loop Vi to ground:

-V_i + I_1*R + I_L*R_L = 0

solving for I_1

I_1 = \frac{V_i - I_L*R_L}{R}

Next is a KVL starting from ground near the negative terminal, and wrapping my way around to the other ground:

-I_R*R - I_R*R + I_R*R +I_L*R_L = 0

solving for I_R

I_R = \frac{I_L*R_L}{R}

now for a KCL at point V_X

I_1 + I_R = I_L

Now I plug my other equations into this equation and solve for I_L

I_L = \frac{V_i}{R}

I don't think this is right because the next part of this problem is to plug in different values for R_L and solve for IL (Vi and R are given), but this equation says R_L doesn't make a difference.

 

[berkeman]

Maybe use KCL to check your answer. I never liked KVL anyway. The KCL is so much more intuitive for me, and I find it is less prone to omission mistakes.

 

[Number2Pencil]

alright here goes with non-stop KCL:

(+ terminal)

\frac{V_i-V_X}{R} + I_R = \frac{V_X}{R_L}

(Vo terminal)

\frac{V_O - V_X}{R} + \frac{V_O - V_X}{R} = 2*I_R

(- terminal)

\frac{V_X}{R} = \frac{V_O - V_X}{R}

solving this one for V_O
2*V_X = V_O

stick this in (Vo terminal) equation, solve for I_R:

I_R = \frac{V_X}{R}

slam this back into first equation, solve for V_X

V_X = \frac{R_L * V_i}{R}

put this into a I_L = \frac{V_X}{R_L} equation and BOOM:

another I_L = \frac{V_i}{R} ...Well this worksheet is dumb for asking me to plug in different values for R_L

 

[berkeman]

Get the same answer with two different approaches, and you can feel good about your answer, right? And I'll bet you're starting to like the KCL better about now, right?

 

[Number2Pencil]

Get the same answer with two different approaches, and you can feel good about your answer, right? And I'll bet you're starting to like the KCL better about now, right?

I felt pretty good about it until my professor said it was wrong...then checked his notes...then told me it was right (this kind of thing happened twice in lab!) it's the same professor who gave an unsolvable op-amp design test problem...I get the feeling I might have to come to this forum for lots of help this semester lol. I hope I'm not wearing out my welcome.

But yeah, I like KCL because it's difficult to screw it up