sliinky
- 3
- 0
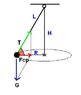
A mass of 80g is moving in a horizontal circle supported by a string 1.2m long suspended from a fixed point in the centre of the circle. The mass completes each revolution in 0.85s. Calculate the tension in the string.
Relevant equations: I'm not entirely sure, but these were the ones I was considering:
T = 2∏R/v
F = mg
ω = 2∏ / T
I think that I need to find the angle between the string and the horizontal, but I don't know how to do that. I've got the hypotenuse of the triangle which is 1.2m..
I also calculated ω using the above equation and got 7.39rad/s. But now I'm lost. Help?
Relevant equations: I'm not entirely sure, but these were the ones I was considering:
T = 2∏R/v
F = mg
ω = 2∏ / T
The Attempt at a Solution
I think that I need to find the angle between the string and the horizontal, but I don't know how to do that. I've got the hypotenuse of the triangle which is 1.2m..
I also calculated ω using the above equation and got 7.39rad/s. But now I'm lost. Help?