Sylvia
- 30
- 1
Homework Statement
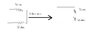
Ignore the internal resistance of the battery and assume it is merely a battery. Calculate the equivalent resistance of the circuit.
Homework Equations
1/Req = 1/R + 1/R ... (parallel)
Req = R + R ... (series)
The Attempt at a Solution
I know this is fairly simple but I don't understand how you would calculate the equivalent resistance for the three resistors (3.2 ohms, 7.1 ohms, 5.8 ohms). I assumed they were in series and simply added them, and then added 1.0 ohms and 4.5 ohms to get the total resistance. I think this is wrong, can someone explain how you would go about calculating the Req?