Gillian
- 2
- 0
For the circuit shown in the figure, the switch S is suddenly closed with the capacitor uncharged. After one time constant, the charge on the capacitor is closest to:
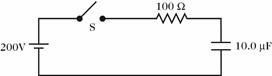
a) 2.0 mC
b) 0.74 mC
c) 1.0 mC
d) 1.3 mC
e) 0.00 mCRelevant Formulas
q = Q⋅(1-e-τ/R⋅C)
τ = RC
My Attempt
q = Q(1-e-τ/T)
q = (10⋅10-6)(1-e-1)
q = (10⋅10-6)(1-.36788)
q = (10⋅10-6)(0.632)
q = 6.32⋅10-6 C = 0.00632 mC
I am not sure how else I would approach this problem. Any suggestions?
a) 2.0 mC
b) 0.74 mC
c) 1.0 mC
d) 1.3 mC
e) 0.00 mCRelevant Formulas
q = Q⋅(1-e-τ/R⋅C)
τ = RC
My Attempt
q = Q(1-e-τ/T)
q = (10⋅10-6)(1-e-1)
q = (10⋅10-6)(1-.36788)
q = (10⋅10-6)(0.632)
q = 6.32⋅10-6 C = 0.00632 mC
I am not sure how else I would approach this problem. Any suggestions?