Calculating Current in RC Circuit with Closed Switch

AI Thread Summary
To calculate the current through R2 immediately after the switch is closed in an RC circuit, the voltage across the initially uncharged capacitor is zero. Given the capacitor value of 7.95 x 10^(-6) F, the resistances R1 at 27.5 Ohm and R2 at 10.5 Ohm, the total voltage from the source is 20.0 V. The current can be determined using Ohm's law, considering only R1 since the capacitor acts as a short circuit at that moment. The discussion emphasizes the importance of understanding the initial conditions of the circuit components.
arl146
Messages
342
Reaction score
1

Homework Statement


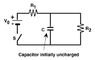
What is the current through R2 immediately after the switch S is closed?
C = 7.95x10^(-6) F , R1 = 27.5 Ohm , R2 = 10.5 Ohm , and Vo = 20.0 V


Homework Equations


I don't know what to use?


The Attempt at a Solution


I thought maybe I use two loops, the left and right and then a junction? I don't know if I have to do a matrix or what for this. Maybe I'm missing something simple here?
 

Attachments

  • prob05av1.gif
    prob05av1.gif
    2.8 KB · Views: 479
Physics news on Phys.org
Please help !
 
Something simple. What's the voltage across the initially uncharged capacitor immediately after the switch is closed?
 
gneill said:
Something simple. What's the voltage across the initially uncharged capacitor immediately after the switch is closed?

Well they say C= 7.95 x 10^(-6) F what is that number for? I don't know.. :(
if it is uncharged is it just zero ?
 
Oh, okay, I got it. It's just zero then. Thanks :D
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Determining Current Direction in a Charging RC Circuit
Replies
1
Views
2K
Calculating Charge and Time in a Discharging RC Circuit
Replies
3
Views
2K
RC Circuit with parallel resistor
Replies
6
Views
3K
How to calculate R1 and R2 in this RC circuit
Replies
3
Views
3K
Current of RC Circuit After Switch is Opened
Replies
3
Views
3K
Need help finding current on RC circuit
Replies
5
Views
7K
Correct statement about series RC circuit
Replies
4
Views
2K
Discharge of a capacitor and current in an RC circuit
Replies
13
Views
3K
Why do the headlights on the car become dim when the car is starting?
Replies
4
Views
2K
Solve RC Circuit Problem: 45V -> 10V in 4.21ms
Replies
4
Views
8K

Hot Threads

Recent Insights

Back
Top