Reason
- 20
- 0
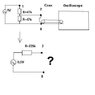
First take a look at the attachment (See reply below). We have to take the oscilloscope's impedance and the coaxial cable's impedance into account. And then we have to calculate the cutoff frequency of this.
Given: Oscilloscope: R=1M Ohm // C=25pF
Coaxial Cable: R=75 Ohm and C=68pF/m with L=0.85m
C=57.8pF
My problem is that I don't know how to draw this. R and C from the Coaxial cable, are they serial or parallel? And the coaxial cable's impedance is that serial or parallel to the oscilloscope's impedance?
If I know that, I can calculate the cutoff frequency and the voltages with different frequencies, but now I'm stuck. Thanks in advance.
Given: Oscilloscope: R=1M Ohm // C=25pF
Coaxial Cable: R=75 Ohm and C=68pF/m with L=0.85m
C=57.8pF
My problem is that I don't know how to draw this. R and C from the Coaxial cable, are they serial or parallel? And the coaxial cable's impedance is that serial or parallel to the oscilloscope's impedance?
If I know that, I can calculate the cutoff frequency and the voltages with different frequencies, but now I'm stuck. Thanks in advance.
Last edited: