flash21
- 4
- 0
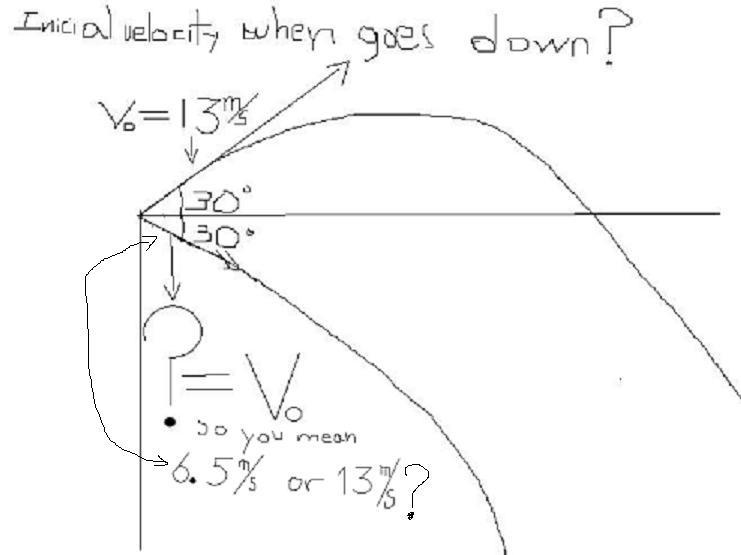
some body help me...it is very simple...somebody throws two rocks from the top of a hill, one above the horizontal line and the other rock below the horizontal line, at an angle of 30 degrees for both rocks and the inicial speed is 13m/s for both rocks as well...the quiestion is how far does the rock 1 is from rock two when they both touch the ground..(rock 1 is the one below horizontal line...rock 2 over the hor...line)...wht i do not know is if wheter rock one(going down) has an inicial speed of 6.5m/s or 13m/s...by the way 6.5m/s comes from the inicial vertical velocity= (sin30)(13m/s)...