davidphysics
- 11
- 0
Hey. This is my first post... here's my question [Diagram Attached]:
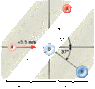
The drawing shows a collision between two pucks on an air-hockey table. Puck A has a mass of 0.028 kg and is moving along the x-axis with a velocity of +5.5 m/s. It makes a collision with puck B, which has a mass of 0.068 kg and is initially at rest. After the collision, the two pucks fly apart with the angles shown in the drawing.
Find the final speed of
(a) puck A and
(b) puck B. [both in m/s]
I am having trouble with this and although I know to use conservation of momentum, should I assume its elastic?
If you could post an explanation that would be great, but I would also like a final answer in numbers please.
The drawing shows a collision between two pucks on an air-hockey table. Puck A has a mass of 0.028 kg and is moving along the x-axis with a velocity of +5.5 m/s. It makes a collision with puck B, which has a mass of 0.068 kg and is initially at rest. After the collision, the two pucks fly apart with the angles shown in the drawing.
Find the final speed of
(a) puck A and
(b) puck B. [both in m/s]
I am having trouble with this and although I know to use conservation of momentum, should I assume its elastic?
If you could post an explanation that would be great, but I would also like a final answer in numbers please.