AriAstronomer
- 46
- 1
Homework Statement
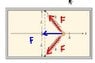
A particle is attached between two identical springs on a
horizontal frictionless table. Both springs have spring
constant k and are initially unstressed. (a) If the particle
is pulled a distance x along a direction perpendicular to
the initial configuration of the springs, as in Figure
P7.66, show that the force exerted on the particle by the
springs is:
F = -2kx(1 - x/(sqrt[x^2 + L^2])
I've attached a printed screen that includes Figure P7.66.
Homework Equations
The Attempt at a Solution
So I know new stretched length is sqrt(x^2 + L^2), forces in y direction cancell, x is multiplied by 2.
New stretched length is L' = sqrt(x^2 + L^2) - L.
F = -kx = -2k[sqrt(x^2 + L^2) - L].
Now here's where I get stuck. It seems like to get the right answer, I need to multiply this by a factor of x/sqrt(x^2 + L^2)...why?
Thanks,
Ari