JudahZ
- 3
- 0
Hey Guys,
So in the attached image I'm trying to determine what the rpm of the 60 tooth gear will be given the 8.4" tire will be rotating at .68 rpm, everything else is just an assumption on my part.
I'm assuming the following which is probably wong:
The tire being rotated at .68 rpm will result in the .5" linked shaft rotating at 11.45 rpm. I'm dividing the circumference of the tire by the circumference of the shaft and multiplying by the rpm of the tire to arrive at 11.45 rpm.
If the .5" shaft is rotating at 11.45 rpm for the purpose of calculations will the 60 tooth gear also be rotating at 11.45 rpm? Sorry, I obviously suck @ life.
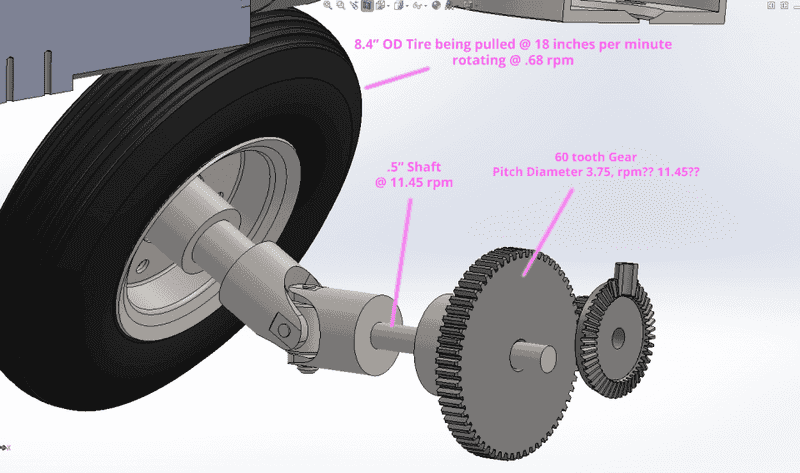
So in the attached image I'm trying to determine what the rpm of the 60 tooth gear will be given the 8.4" tire will be rotating at .68 rpm, everything else is just an assumption on my part.
I'm assuming the following which is probably wong:
The tire being rotated at .68 rpm will result in the .5" linked shaft rotating at 11.45 rpm. I'm dividing the circumference of the tire by the circumference of the shaft and multiplying by the rpm of the tire to arrive at 11.45 rpm.
If the .5" shaft is rotating at 11.45 rpm for the purpose of calculations will the 60 tooth gear also be rotating at 11.45 rpm? Sorry, I obviously suck @ life.
Last edited: