wr1015
- 53
- 0
A rectangular loop of wire 24 cm by 72 cm is bent into an L shape, as shown in Figure 23-37. The magnetic field in the vicinity of the loop has a magnitude of 0.034 T and points in a direction = 22° below the y axis. The mangnetic field has no x component. Find the magnitude of the magnetic flux through the loop.
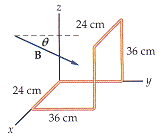
why doesn't the formula \phi = BA cos \theta work, when A = (.36)^2, \theta = 22, and B = .034T?? what am i missing here?
why doesn't the formula \phi = BA cos \theta work, when A = (.36)^2, \theta = 22, and B = .034T?? what am i missing here?
Last edited:
 i see what you mean now.. thank you for your help, i really wished my book and professor would've explained this a lot better especially when dealing with different planes
i see what you mean now.. thank you for your help, i really wished my book and professor would've explained this a lot better especially when dealing with different planes