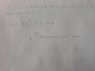Martin89
- 25
- 1
Homework Statement
Homework Equations
The Attempt at a Solution
Hi All,
My problem is that when I calculate this integral or use software to do it for me I get (3*i*pi)/16, when I've been told that the answer is 1/2i giving a probability of 1/4. Would someone be able to point out where my mistake is.
Thanks