InterestedGuy
- 4
- 0
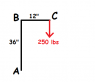
I'm trying to figure out the stress on member AB in the attached diagram, given a load of 250lbs at point C.
Obviously there is a torque of 250ft-lbs at point B, but I'm not sure how to translate that into stress on member AB? My end goal is to size member AB so that the stress is stays below the yield strength, but I'm not sure how the calculate the stress.
Can anyone help?
Thanks,
Edit:
I've been thinking about this and I think the answer is pretty simple. Let me know if this is correct.
I essentially have a force vector AC. 250lbs represents the x component of this force. Thus the y component is 83.3 lbs at point B. From there I can figure out the bending stress on AB as it is essentially a cantilever.
Does that make sense?
Obviously there is a torque of 250ft-lbs at point B, but I'm not sure how to translate that into stress on member AB? My end goal is to size member AB so that the stress is stays below the yield strength, but I'm not sure how the calculate the stress.
Can anyone help?
Thanks,
Edit:
I've been thinking about this and I think the answer is pretty simple. Let me know if this is correct.
I essentially have a force vector AC. 250lbs represents the x component of this force. Thus the y component is 83.3 lbs at point B. From there I can figure out the bending stress on AB as it is essentially a cantilever.
Does that make sense?
Attachments
Last edited: