Calculating Stress in Non-Vertical Structural Members: Does Orientation Matter?

[illwerral]

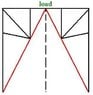
So in my physics class we built cardboard chairs as a project. Part of the assignment is to draw in all of the stresses, and then do calculations to see how much stress exists in all of the structural members. One of my main structural members is a triangle, its peak attaches to the main panel that one would sit on. All of the calculations are easy except this one, because it is the only structural member that is not vertical, and my question is: does it matter this piece isn't vertical? Like would I say (force parallel to member)/area to find stress, or would it just be (force)/area like a vertical piece?

I've attached an image to make my question more clear...I'm looking to find the stress on the red member. I didn't include values because arithmetic isn't a problem.

Thanks!

 

[Pyrrhus]

Well the stress that can be presented in a structure (in no particular order):

Shear
Torsional
Bending
Tension
Compression

In your case, the joint (or the peak of the triangle) could be modeled as a node, and with the equations of equilibrium it can be solved which axial loads go through each of the members. After you find each load along the axis of the members, you can use the cross section area of the member in your known formula $\sigma = \frac{P}{A}$

 

[illwerral]

I haven't actually heard of the term node used in this context. We went over stress/strain pretty briefly, so I don't have much of a knowledge of this stuff yet. Would you mind elaborating a little bit?

 

[Pyrrhus]

What i mean by node is the connection between the chair and the two structural members. The point where they converge or that they are concurrent at said point. I'll elaborate more after i see the geometric design of the structure.

 

[illwerral]

I'll elaborate more after i see the geometric design of the structure.

My diagram's available to look at now. And thanks for the help!

 

[Pyrrhus]

I don't understand the diagram

 

[illwerral]

It is the side view of the chair, showing the supports used. The dotted line is just an axis of symmetry. I guess stool is a better word for this structure, if that helps.

I know its an odd design for a chair but we were only allowed using corrugated cardboard, and so a normal design could never be strong enough for the assignment.

 

[Pyrrhus]

It is the side view of the chair, showing the supports used. The dotted line is just an axis of symmetry. I guess stool is a better word for this structure, if that helps.

I know its an odd design for a chair but we were only allowed using corrugated cardboard, and so a normal design could never be strong enough for the assignment.

I'm sorry, i haven't replied. I've been busy. Anyway are those bars or complete filled triangular pieces?. This will affect the stress distribution.

 

[illwerral]

The red lines are rectangular sheets arranged as a triangular prism, with two triangular sheets to fill in what would be the bases of the prism.

 

[Pyrrhus]

Heh, so have you taken a Structural Analysis course?, this is not a trivial stress distribution, like simple chair for example where we have 1 shell supported by 4 columns.