Ali0086
- 14
- 0
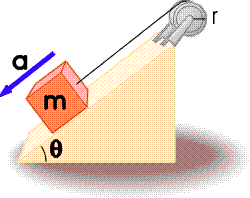
An m = 12.4kg mass is attached to a cord that is wrapped around a wheel of radius r = 10.0cm (see the figure below). The acceleration of the mass down the frictionless incline is measured to be a = 2.10m/s^2.
a) Assuming the axle of the wheel to be frictionless, and the angle to be θ = 36.2deg determine the tension in the rope.
b) Determine the moment of inertia of the wheel
c)Determine angular speed of the wheel 2.04s after it begins rotating, starting from rest.
All in all I just have a lot of trouble drawing free body diagrams and just figuring out how to approach a problem with my given set of known variables.
On my initial attempt for part a) I tried drawing a free body diagram but I didn't know if I should add the value I get from mgsin(theta) to the value that I got for F (I used m*a to get that value).
I've uploaded my attempt at a solution and I didn't get very far. I feel like there's a process at solving these questions but I just don't get it. Any help would be appreciated.
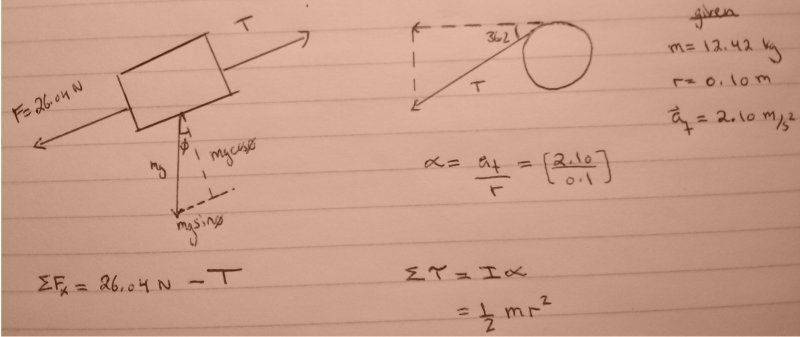
a) Assuming the axle of the wheel to be frictionless, and the angle to be θ = 36.2deg determine the tension in the rope.
b) Determine the moment of inertia of the wheel
c)Determine angular speed of the wheel 2.04s after it begins rotating, starting from rest.
All in all I just have a lot of trouble drawing free body diagrams and just figuring out how to approach a problem with my given set of known variables.
On my initial attempt for part a) I tried drawing a free body diagram but I didn't know if I should add the value I get from mgsin(theta) to the value that I got for F (I used m*a to get that value).
I've uploaded my attempt at a solution and I didn't get very far. I feel like there's a process at solving these questions but I just don't get it. Any help would be appreciated.