Calculating the Horizontal Force for a Non-Slipping Wedge

[ElectricMile]

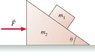
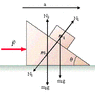
Find an expression for the magnitude of the horizontal force in the figure for which does not slip either up or down along the wedge. All surfaces are frictionless.




I am a little confused, what is this question really asking? i have attempted sevral trig equations but i can't get the answer correct...anyone point me in the right way?

 

[Doc Al]

First identify all the forces acting on the block. Then apply Newton's 2nd law. (Hint: vertical forces must add to zero, otherwise the block will accelerate in the vertical direction.)

 

[ElectricMile]

im still so confused on this problem...ok i have the forces for the block and the wedge the same, they both have a line pointing up and down, and pointing right for the force...but I am completely lost on how to begin solving this problem.

 

[Leong]

If m_1 is not to slip in any direction, it will move forward together with m_2 with accelerelation a. Upward and right direction is choosen to be y and x axis.
Consider m_1:
y component :
N_{1}sin(90-\theta)+(-m_{1}*g)=0
N_{1}cos\theta=m_{1}*g…(1)
x component :
N_{1}cos(90-\theta)-m_{1}*a=0
N_{1}sin\theta=m_{1}*a…(2)
Consider m_2:
x component:
F+(-N_{1}sin\theta)=m_{2}*a
F-N_{1}sin\theta=m_{2}*a…(3)
(2) into (3):
F-m_{1}*a=m_{2}*a
F =a*(m_{1}+ m_{2})…(4)
(2) divided by (1) :
tan\theta=\frac{a}{g}…(5)
(5) into (4) :
F=gtan\theta(m_{1}+ m_{2})