Calculating the Intersection of Two Cylinders at Right Angle

[stunner5000pt]

Homework Statement

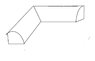
Consider two quarters of a cylinder of radius R. What is the volume of a the intersection of a two quarters of two cylinders if the quarters meet at a right angle? Two sides of the bounded region will be rectangular according to this arrangement. (see the diagram when it gets approved)

2. The attempt at a solution
I need to do this in Cartesian coordinates so here goes

let the Z axis be straight up, the X axis out of the page an the Y axis parallel to the page.

For the cylindrical part parallel to the X axis
V = \int_{0}^{r} dx \int_{0}^{r} \int_{0}^{\sqrt{r^2 - y^2}} dy dz

For hte cylindrical parallel to the Y axis
V = \int_{0}^{r} dy \int_{0}^{r} \int_{0}^{\sqrt{r^2-x^2}} dx dz
And the find the volume i need to subtract the above two??

 

[stunner5000pt]

Any help would be greatly appreciated!

 

[danni7070]

I had simular problem once, but I was given that the volume of the whole region was eight times the part volume.

V = 8 \int_{0}^{r} {(r^2-z^2)}dz

V = 8(r^2z-(z^3/3) |r

V = (16*r^3)/3 units.

Hope you figure this one out.

 

[stunner5000pt]

I had simular problem once, but I was given that the volume of the whole region was eight times the part volume.

V = 8 \int_{0}^{r} {(r^2-z^2)}dz

V = 8(r^2z-(z^3/3) |r

V = (16*r^3)/3 units.

Hope you figure this one out.

dont understand how you got your integrand to be r^2 -z^2?

Adn waht do you mean by 8 times part volume?

 

[danni7070]

If you "slice" horizontally at height z above the xy-plane then the slice has a side equal to

{\sqrt{(r^2-z^2)}} and a area A(z) = r^2-z^2


The slice is a rectangle with equal size on all sides. (what is it called in english?)

where a = {\sqrt{r^2-z^2} is on side of that rectangle.

But you are wondering why ? I can't really explain it but when you have circular solids you use {\sqrt(r^2-z^2)} where r = radius of the circle.

From the figure you posted these are two "1/4-th" circles

I'm sure someone can explain it better then me here.