marand2017
- 3
- 1
Member advised to use the homework template for posts in the homework sections of PF.
Hi there,
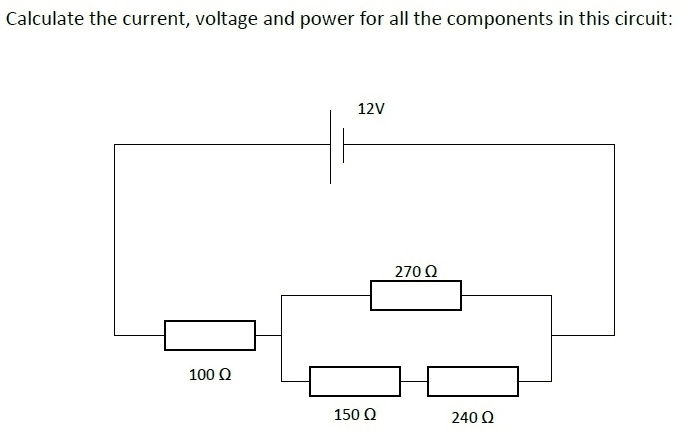 The problem asks me to calculate the Voltage, Current and Power of each component within the circuit. I have already calculated the following:
The problem asks me to calculate the Voltage, Current and Power of each component within the circuit. I have already calculated the following:
V total = 12 Volts
R total = 259.54 Ohm
I total = 0.046 Amps
I am confused as to how I am supposed to calculate the voltage drop across each resistor. As the circuit contains parallel resistors followed by one in series it is a bit confusing and would greatly appreciate the help. I know how to calculate if all resistors are in parallel or if all are in series but a combination of each is confusing as I need the voltage drop across each resistor.
Thanks
Marco
V total = 12 Volts
R total = 259.54 Ohm
I total = 0.046 Amps
I am confused as to how I am supposed to calculate the voltage drop across each resistor. As the circuit contains parallel resistors followed by one in series it is a bit confusing and would greatly appreciate the help. I know how to calculate if all resistors are in parallel or if all are in series but a combination of each is confusing as I need the voltage drop across each resistor.
Thanks
Marco
Last edited by a moderator: