Joosh
- 7
- 4
Hey, folks! So upon studying for my Physics final tomorrow, I came across this question on the practice exam, which I know the answer is D from the solution key. However, I'm not sure how to get that for the answer.
1. Homework Statement
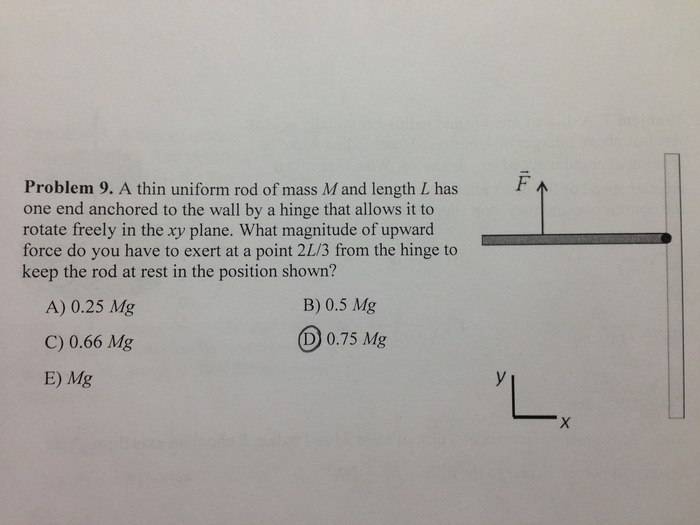
τ = rA × Fnet
LA = Ltrans, A + Lrot
Ltrans = rcm × Ptot
Lrot = r1 × p1 + r2 × p2 + ...
I personally don't entirely know where to start. I'm going to guess this is a torque-related question, but I'm not sure if that's the right way to go at it.
1. Homework Statement
Homework Equations
τ = rA × Fnet
LA = Ltrans, A + Lrot
Ltrans = rcm × Ptot
Lrot = r1 × p1 + r2 × p2 + ...
The Attempt at a Solution
I personally don't entirely know where to start. I'm going to guess this is a torque-related question, but I'm not sure if that's the right way to go at it.