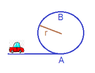
Calculating Velocity for a Loop the Loop

AI Thread Summary
To calculate the minimal velocity at point A to reach point B in a loop-the-loop scenario without friction, the correct formula is v = sqrt(5gr), which accounts for the necessary centripetal force at the top of the loop. While the initial calculation suggested v = sqrt(4gr), this does not provide enough speed to counteract gravity and maintain contact with the track. The discussion emphasizes that without sufficient velocity, the normal force would become negative, indicating that the car would not stay on the track. The centripetal force required at point B must be positive to ensure the vehicle remains on the path. Thus, achieving the correct speed is crucial for successfully navigating the loop.
motti
Messages
2
Reaction score
0
Hi,

i need to calculate the minimal velocity at point A to reach point B
Not asked to complete full loop, There is no friction.

I guess (mv^2)/2 = mg*2r >>> v = sqrt(4gr), my friend say v = sqrt(5gr)

Thanks.
 

Attachments

  • 55.png
    55.png
    1.2 KB · Views: 492
Physics news on Phys.org
You have used an energy argument. With this argument, what would be the speed at B? What is the corresponding required centripetal force at B? What is the actual centripetal force at B?
 
Probably zero..
i know that its 5gr if i want to "loop the loop" - but i only want to reach the top..
 
The point is that you need that speed to reach the top. Otherwise the acceleration due to gravity is too large and the normal force from the track would have to be negative (with positive direction defined as being towards the loop center) in order to keep the car on track. So unless the car is somehow fixed to the track (as in some roller coasters that at points have "negative gs") you will need the extra speed in order to actually reach B.
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'Calculation of Tensile Forces in Piston-Type Water-Lifting Devices at Elevated Locations'

Thread 'Calculation of Tensile Forces in Piston-Type Water-Lifting Devices at Elevated Locations'

Figure 1 Overall Structure Diagram Figure 2: Top view of the piston when it is cylindrical A circular opening is created at a height of 5 meters above the water surface. Inside this opening is a sleeve-type piston with a cross-sectional area of 1 square meter. The piston is pulled to the right at a constant speed. The pulling force is（Figure 2）： F = ρshg = 1000 × 1 × 5 × 10 = 50,000 N. Figure 3: Modifying the structure to incorporate a fixed internal piston When I modify the piston...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Loop the Loop Problem Solution | N > 0, Energy Conservation Method
Replies
8
Views
3K
Loop problem with skier on ramp going into a loop-the-loop
Replies
13
Views
2K
Force on rectangular loop by a current in a long straight wire
Replies
4
Views
2K
Why does the speed change at the bottom of the loop-the-loop?
Replies
5
Views
2K
Apparent weight problem (kinematics + conservation of Energy + Newton's laws)
Replies
41
Views
3K
Starting height of marble rolling around a loop the loop
Replies
12
Views
12K
Circular motion - ball in a loop
Replies
19
Views
4K
Force to apply to a loop moving away from a current-carrying wire
Replies
4
Views
2K
Proper use of inequality symbols in equations to do with circular motion
Replies
2
Views
1K
What is the induced magnetic force on this closed current loop?
Replies
12
Views
2K

Hot Threads

Recent Insights

Back
Top