Ntothaate
- 2
- 0
Homework Statement
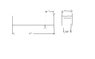
This is not a homework problem, but something i can't figure out how to calculate. Basically I have what is similar to a cantilever beam setup with an extension. what i need to figure out is what the vertical forces are at the two points(triangles on the attached paint drawing), and how I would Calculate that. There is no force added at any point, so it needs to be calculated solely off the mass of the beam. I don't know the mass so at this point i can just make one up as M=1lb, or whatever unit you would like. thank you in advance