mahmud_dbm
- 17
- 0
Member warned about posting without the template and with no effort
I have been trying to solve an integration that i have
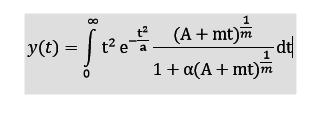
I am not even sure if it's possible. Here, A, m, alpha, a these are constants. I have tried few methods, but couldn't find any way out. I would appreciate any help.
I am not even sure if it's possible. Here, A, m, alpha, a these are constants. I have tried few methods, but couldn't find any way out. I would appreciate any help.