JI567
- 173
- 0
Hi,
Can somebody tell me if my kinetic energy (T) and potential energy of spring (V) for this system in matrix form is correct or wrong,
m1= 2, k1 =5, m2 = m2, k2 = k2
T = 1/2 (2* q1'^2+ m2* q2'^2) so in matrix form it was 1/2(q'^T) (2 0 *( q')
0 m2)
V = 1/2 (5*q1^2+k2(q2-q1)^2) = 1/2 ((5+k2)* q1^2- 2*k2*q1*q2 + k2*q2^2) so in matrix form it was
1/2 (q^T) ( 5+k2 -k2 * (q)
-k2 k2)
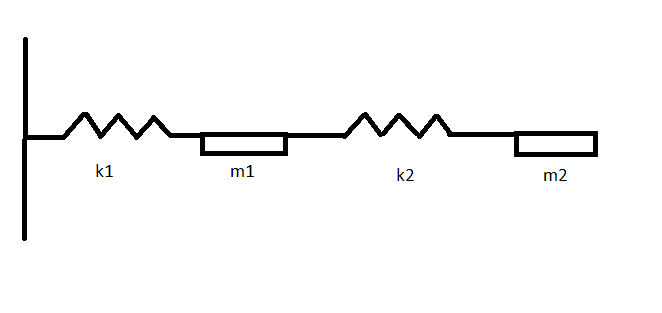
Can somebody tell me if my kinetic energy (T) and potential energy of spring (V) for this system in matrix form is correct or wrong,
m1= 2, k1 =5, m2 = m2, k2 = k2
T = 1/2 (2* q1'^2+ m2* q2'^2) so in matrix form it was 1/2(q'^T) (2 0 *( q')
0 m2)
V = 1/2 (5*q1^2+k2(q2-q1)^2) = 1/2 ((5+k2)* q1^2- 2*k2*q1*q2 + k2*q2^2) so in matrix form it was
1/2 (q^T) ( 5+k2 -k2 * (q)
-k2 k2)