Can these diagrams describe an electrostatic field in a charge free space

[GalMichaeli]

Homework Statement

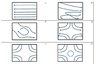
Determine if the following diagrams may describe an electrostatic field in a charge-free space. The rectangles are the spaces under consideration. In the first four diagrams there are field lines while in the last two there are equipotential lines

Homework Equations

For the field lines, I used Gauss's law (in cgs):
div(E) = 4∏ρ
And for the potential diagrams, Earnshaw's theorem.

The Attempt at a Solution

I deduced that the upper-left and lower-left diagrams can describe such a field, but that was wrong.

Thanx.

 

[Simon Bridge]

How did you make that deduction?
If we don't know your reasoning, we cannot figure out how best to help you.
(It looks like they want you to show you know how to draw flux diagrams.)

Hint: for a diagram to be invalid, it must be (a) not a valid flux diagram, or (b) be a flux diagram that has a charge in it.