nashsth
- 16
- 0
Hi everyone, I want to rotate this (see attached image) platform at a speed of 20 RPM. To this end, I have to calculate the torque and power of a motor required. I have done preliminary calculations, however the numbers I'm getting doesn't seem right. For example, I'm getting that the torque required is 0.15 N*m, and the power is ~0.3 W.
Here are the details:
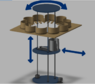
In the image, the brown part is stationary, and only the blue discs are rotated using a motor, which is shown in the lower right. So basically, the motor at the lower right corner is connected to the blue disc (via e.g. a belt). Then, that blue disc is attached to the middle blue disc with the silver hollow cylindrical object via the three tall rods, and this disc is connected to the top-most disc also via the three rods.
For context, the idea is to use the brown part as a shelf in which canned goods are stored. The central disc system is a mechanism for lifting these cans. The central blue disc (with the hollow cylindrical object) is the platform which can move up and down (between the upper and lower blue discs, as shown by the up-down arrow), it can rotate (as shown by the curved arrows), and the cylindrical object (i.e. the "claw") can extend and retract (as shown by the left-right arrow).
The question is, how much torque and power must the motor provide to ensure that the assembly rotates at 20 RPM, and takes 0.5 seconds to accelerate from 0 RPM to 20 RPM? The mass of each of the blue disks is estimated to be 1 kg, and the mass of the three rods is estimated to be 1 kg in total, and the claw can support a canned good whose mass is 1 kg at most.
So I approached this problem by first noting that Power = Tau * Omega, where Tau is the torque and Omega is the angular velocity.
Next, Tau = I*alpha, where I is the moment of inertia of the entire system, and alpha is the angular acceleration.
To calculate the moment of inertia, I used I = 0.5*M*R^2, where M is the mass of the object in consideration, and R is the radius. For the disks, the radius is ~6 inches (0.15 meters), and the mass is 1 kg, as noted above. For the canned good, the mass is also 1 kg, and the radius is ~2 inches (0.051 meters). Hence, the moment of inertia for each disk is 0.01125 kg*m^2, and the moment of inertia for the can is 1.3*10^-3 kg*m^2. The total moment of inertia for the three disks and the can is 0.035 kg*m^2. I ignored the moment of inertia for the three rods because they're incredibly small (on the order of -6).
The angular acceleration is just 20 RPM / 0.5 seconds = 2.1 rad/sec / 0.5 sec = 4.2 rad/sec^2
Then, the torque would be: Tau = 0.035*4.2 = 0.147 N*m
The power would be: Power = (0.147 N*m) * (2.1 rad/sec) = 0.31 W
I feel that these values for torque and power are too small to be able to rotate my assembly, but I am not a mechanical engineer so I don't have a good feel for these kinds of things. If anyone could check over my numbers and/or suggest a new way to approach the problem, I would greatly appreciate it.
Here are the details:
In the image, the brown part is stationary, and only the blue discs are rotated using a motor, which is shown in the lower right. So basically, the motor at the lower right corner is connected to the blue disc (via e.g. a belt). Then, that blue disc is attached to the middle blue disc with the silver hollow cylindrical object via the three tall rods, and this disc is connected to the top-most disc also via the three rods.
For context, the idea is to use the brown part as a shelf in which canned goods are stored. The central disc system is a mechanism for lifting these cans. The central blue disc (with the hollow cylindrical object) is the platform which can move up and down (between the upper and lower blue discs, as shown by the up-down arrow), it can rotate (as shown by the curved arrows), and the cylindrical object (i.e. the "claw") can extend and retract (as shown by the left-right arrow).
The question is, how much torque and power must the motor provide to ensure that the assembly rotates at 20 RPM, and takes 0.5 seconds to accelerate from 0 RPM to 20 RPM? The mass of each of the blue disks is estimated to be 1 kg, and the mass of the three rods is estimated to be 1 kg in total, and the claw can support a canned good whose mass is 1 kg at most.
So I approached this problem by first noting that Power = Tau * Omega, where Tau is the torque and Omega is the angular velocity.
Next, Tau = I*alpha, where I is the moment of inertia of the entire system, and alpha is the angular acceleration.
To calculate the moment of inertia, I used I = 0.5*M*R^2, where M is the mass of the object in consideration, and R is the radius. For the disks, the radius is ~6 inches (0.15 meters), and the mass is 1 kg, as noted above. For the canned good, the mass is also 1 kg, and the radius is ~2 inches (0.051 meters). Hence, the moment of inertia for each disk is 0.01125 kg*m^2, and the moment of inertia for the can is 1.3*10^-3 kg*m^2. The total moment of inertia for the three disks and the can is 0.035 kg*m^2. I ignored the moment of inertia for the three rods because they're incredibly small (on the order of -6).
The angular acceleration is just 20 RPM / 0.5 seconds = 2.1 rad/sec / 0.5 sec = 4.2 rad/sec^2
Then, the torque would be: Tau = 0.035*4.2 = 0.147 N*m
The power would be: Power = (0.147 N*m) * (2.1 rad/sec) = 0.31 W
I feel that these values for torque and power are too small to be able to rotate my assembly, but I am not a mechanical engineer so I don't have a good feel for these kinds of things. If anyone could check over my numbers and/or suggest a new way to approach the problem, I would greatly appreciate it.
 . Three seconds/revolution is of course 2.1 rad/s.
. Three seconds/revolution is of course 2.1 rad/s.