Can You Solve This Circuit with Mutual Inductance and Capacitance?

In summary, The conversation discusses the formulation of equations to find functions for current in a system with mutual inductance. The equations involve a mutual inductance constant, as well as the variables of charge, inductance, and current. The question of how to find the charge on the capacitor is raised, but it is noted that Q is just a characteristic of the capacitor and there is likely a relation between Q and the currents. It is suggested to find a third equation to solve for the three variables.
  • #1
Slightly
29
0

Homework Statement



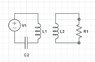
In the given picture, I need to formulate some kind of solution to find functions for the current, knowing that the two inductances create a mutual inductance (coupling)

The Attempt at a Solution



I start by formulating these two equations where M is the mutual inductance.

For the left, E= Q/C + L1*dI1/dt - M*dI2/dt
and
for the right, 0= L2*dI2/dt + R*I2 - M*dI1/dt

Does this look okay so far, and where should I go from here?
 

Attachments

  • circuit 1.jpg
    circuit 1.jpg
    10.8 KB · Views: 401
Physics news on Phys.org
  • #2
What is Q?. Find it and the question will be solved.
 
  • #3
Q is just the charge on the capacitor
 
  • #4
Is there a relation between Q and I1, I2 ?
 
  • #5
I'm sure there is one, but Q is just a characteristic of the capacitor.
 
  • #6
Slightly said:
I'm sure there is one, but Q is just a characteristic of the capacitor.

The two equations you have made have 3 variables(Q ,I1, I2,) so it can't be solved. Try to get a third equation and you will have 3 equations for three variables.

Hint: The third equation is a relation between I1 and Q. What is it?
 

FAQ: Can You Solve This Circuit with Mutual Inductance and Capacitance?

1. What is an oscillation in a circuit?

An oscillation in a circuit refers to the repetitive back-and-forth movement of electrons or electric current within a circuit. This movement is caused by the exchange of energy between the inductor and capacitor in the circuit.

2. What is the formula for calculating the frequency of oscillations in a circuit?

The formula for calculating the frequency of oscillations in a circuit is f = 1 / (2π√(LC)), where f is the frequency in Hertz (Hz), L is the inductance in Henrys (H), and C is the capacitance in Farads (F).

3. What factors affect the frequency of oscillations in a circuit?

The frequency of oscillations in a circuit is affected by the values of inductance and capacitance in the circuit, as well as the applied voltage and the resistance of the circuit. Any changes in these factors will result in a change in the frequency of oscillations.

4. How does the type of circuit affect oscillations?

The type of circuit, such as series or parallel, can affect oscillations in different ways. In a series circuit, the inductance and capacitance values add up, resulting in a lower frequency of oscillations. In a parallel circuit, the inductance and capacitance values are inversely proportional, resulting in a higher frequency of oscillations.

5. What is the significance of oscillations in a circuit?

Oscillations in a circuit are significant because they allow for the production of alternating current, which is used to power various electronic devices. They also play a crucial role in the functionality of electronic components such as oscillators, filters, and resonant circuits.

Similar threads

I Mutual inductance in a transformer
Replies
16
Views
2K
Mutual Inductance - Two rectangular loops
Replies
2
Views
5K
Mutual Inductance Between Square and Circle Circuit
Replies
1
Views
2K
Current through ring in solenoid-ring system
Replies
1
Views
922
Accounting for mutual inductance in a Hartley Oscillator
Replies
10
Views
2K
B Antenna induction, oscillating circuit generating EM Waves
Replies
6
Views
824
Mutual inductance as a psuedo-capacitor?
Replies
1
Views
1K
Mutual Induction of a solenoid and a coil
Replies
1
Views
2K
Dot convention inductors in series: equation confusion
Replies
6
Views
2K
Mutual inductance coefficient with so little info
Replies
13
Views
2K

Hot Threads

Recent Insights

Back
Top