sa1988
- 221
- 23
Just a quick one - Have I deciphered the wording of this question properly?
All necessary info is in the embedded image.
To me the limits describe a typical 'pyramid in the corner', but the fact it's an integral over the function 'x' is confusing me. Do I just go with it and generate an answer at the end?
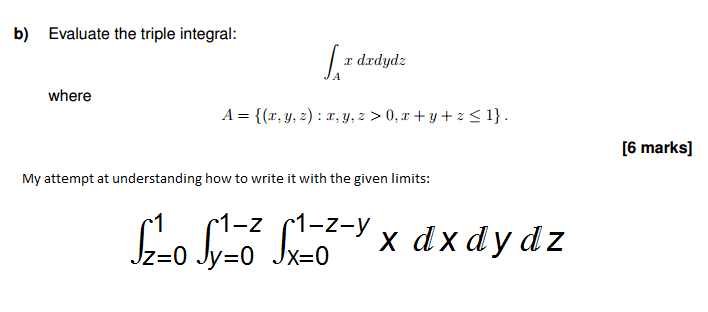
All necessary info is in the embedded image.
To me the limits describe a typical 'pyramid in the corner', but the fact it's an integral over the function 'x' is confusing me. Do I just go with it and generate an answer at the end?
 my nitwit "distinguish" comment is superfluous and I nitwittedly wanted to improve on an integral expression that wasn't wrong in the first place.
my nitwit "distinguish" comment is superfluous and I nitwittedly wanted to improve on an integral expression that wasn't wrong in the first place.