maxipoblete
- 2
- 1
- Homework Statement
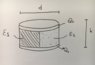
- Two circular parallel metallic plates (diameter d) are separated by a distance "h" . Between the plates, there are two parallel dielectrics with constants ε1 and ε2. At the beginning, the plates have a charge Q0 and -Q0. Calculate the capacitance.
- Relevant Equations
- C=Q/V
Hello, the problem is better illustrated at the picture below.
The capacitor is isolated, with an initial charge Q0. I understand that Q0 does not distribute along the plates homogeneously. How could it be solved with the equivalent parallel circuit?
The capacitor is isolated, with an initial charge Q0. I understand that Q0 does not distribute along the plates homogeneously. How could it be solved with the equivalent parallel circuit?