Capacitors in series and Kirchoff's law

[atyy]

I just said that it's problematic to tak about these plates potentials, because we talk about uniform field that only exists inside the capacitor, and that it's problematic to choose a general point of perspective for both capacitors, to know the potential on each plate.

Yes, that was puzzling to me too. The equilibrium distribution is dependent on the initial charge distribution, but fundamentally, it seemed to me that equilibrium for charged nodes could still be handled by the condition of equilibrium, equipotentiality of connected plates, charge conservation at each node, and the definition of capacitance for each capacitor in series (which if you read below may not be quite right). But the equations I got were unduly messy for such a simple situation.

When you connect two caps in series, the plates that are connected via the conducting leads become One plate, electrically speaking, and that is the language we are speaking here today.

You can extend this model to include any number of caps you wish keeping in mind that where the leads are connected together, there is effectively only one plate in play.

And schroder's comments also indicated a good trick for the equilibrium distribution, but I had trouble getting the trick right with more capacitors

Then I found this interesting comment on Wikipedia: C=Q/V does not apply when there are more than two charged plates, or when the net charge on the two plates is non-zero. To handle this case, Maxwell introduced his "coefficients of potential". If three plates are given charges Q1,Q2,Q3, then the voltage of plate 1 is given by V1 = p11Q1 + p12Q2 + p13Q3, and similarly for the other voltages.
http://en.wikipedia.org/wiki/Capacitance

 

[atyy]

Your assumptions are that both the common node doesn't include other elements drawing current at any time, and that the initial conditions are q_1 = q_2.

Then I found this interesting comment on Wikipedia: C=Q/V does not apply when there are more than two charged plates, or when the net charge on the two plates is non-zero. To handle this case, Maxwell introduced his "coefficients of potential".

The coefficients of potential appear to matter only if the independence assumption is violated. If it is not, I think Phrak gives the correct statement of the two necessary assumptions for applying the capacitors in series formula. The following articles contain an amusing discussion about the violation of the first assumption (which I had not appreciated in my derivation in post #11):

A myth about capacitors in series
L. Kowalski
Phys. Teach. 26, 286 (1988)

Are the textbook writers wrong about capacitors?
A. P. French
Phys. Teach. 31, 156 (1993)

Equal plate charges on series capacitors?
B. L. Illman and G. T. Carlson
Phys. Teach. 32, 77 (1994)

Another in our series on capacitors
A. P. French
Phys. Teach. 32, 262 (1994)

 

[ibc]

The following articles contain an amusing discussion about the violation of the first assumption (which I had not appreciated in my derivation in post #11):

A myth about capacitors in series
L. Kowalski
Phys. Teach. 26, 286 (1988)

Are the textbook writers wrong about capacitors?
A. P. French
Phys. Teach. 31, 156 (1993)

Equal plate charges on series capacitors?
B. L. Illman and G. T. Carlson
Phys. Teach. 32, 77 (1994)

Another in our series on capacitors
A. P. French
Phys. Teach. 32, 262 (1994)

Do you know perhaps where we can find them? (internet, link, or whatever, I'm just not very familiar with knowing where do find such things =x )

 

[atyy]

Do you know perhaps where we can find them? (internet, link, or whatever, I'm just not very familiar with knowing where do find such things =x )

The articles can be found at:
http://scitation.aip.org/tpt/

Unfortunately they require a subscription, and they aren't on arXiv. So I will just quickly describe the most instructive situation I found, from Kowalski's and French's articles.

A) Consider 2 capacitors C1, C2 in series with a constant emf V across X, Z (node Y between the capacitors is labelled for convenience):
X---C1---Y---C2---Z,

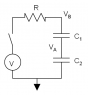
B) Then consider a modification of the above setup, still with C1,C2 and V across X,Z, but now with R1 parallel to C1, R2 parallel to C2:
X---C1---Y---C2---Z
X---R1---Y---R2---Z

We start off with no charged nodes and no current flowing in both situations. In both A and B, there is no current flowing through C1,C2 at steady states. But in B, there is current through R1,R2 at steady state. This causes the steady state voltage between XY and YZ to be different in situations A and B. When one thinks about it carefully, the capacitors are not in series when the circuit is being charged, in the sense that the same current is not flowing through them, which is why the derivation in post #11 fails. Ironically, they are "in series" at steady state when no current flows through C1 and C2! So if we require capacitors in series to be in series at all times, then perhaps the statement of Phrak's first assumption is not strictly necessary (equivalent to the definition of capacitors in series). However it is definitely helpful. Kowalski comments that real capacitors have leak currents, which are modeled by R1, R2, and so one must be careful about modelling a real situation with ideal elements.

So I guess the checklist is:
1) Are the real elements are equivalent to the ideal elements?
2) Is the circuit small enough to apply circuit theory?
3) Are the elements sufficiently small and the distance between the elements sufficiently large to take the independence assumption?
4) Are the capacitors in series? (Phrak's first assumption in post #45)
5) What is the initial charge distribution at the nodes?
- If it is zero, then, for capacitors in series, the charge on connected plates will be equal and opposite, by conservation of charge. (Phrak's second assumption in post #45)
- If the nodes are charged, the equilibrium condition is given by the equillibrium voltage across the series, the equipotentiality of connected plates, charge conservation at each node, and the definition of capacitance for each capacitor in series.