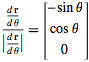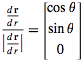shreddinglicks
- 225
- 7
Homework Statement
I want to convert R = xi + yj + zk into cylindrical coordinates and get the acceleration in cylindrical coordinates.
Homework Equations
The Attempt at a Solution
I input the equations listed into R giving me:
R =
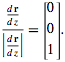
Apply chain rule twice:
The final answer is:
How do I get this final answer? It looks like the terms with sin were dropped. How does this happen?
Attachments
-
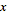 Inline31.gif173 bytes · Views: 756
Inline31.gif173 bytes · Views: 756 -
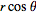 Inline33.gif1.1 KB · Views: 509
Inline33.gif1.1 KB · Views: 509 -
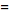 Inline38.gif162 bytes · Views: 498
Inline38.gif162 bytes · Views: 498 -
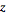 Inline37.gif273 bytes · Views: 480
Inline37.gif273 bytes · Views: 480 -
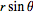 Inline36.gif1 KB · Views: 523
Inline36.gif1 KB · Views: 523 -
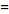 Inline35.gif162 bytes · Views: 496
Inline35.gif162 bytes · Views: 496 -
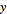 Inline34.gif277 bytes · Views: 464
Inline34.gif277 bytes · Views: 464 -
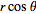 Inline33.gif1.1 KB · Views: 504
Inline33.gif1.1 KB · Views: 504 -
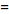 Inline32.gif162 bytes · Views: 720
Inline32.gif162 bytes · Views: 720 -
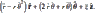 Inline212.gif2 KB · Views: 469
Inline212.gif2 KB · Views: 469 -
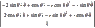 Inline209.gif3.2 KB · Views: 478
Inline209.gif3.2 KB · Views: 478 -
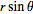 Inline36.gif1 KB · Views: 464
Inline36.gif1 KB · Views: 464