rash219
- 22
- 0
Centripetal Acceleration !
An Engineer wishes to design a curved exit ramp for a toll road in such a way that a car will not have to rely on friction to round the curve without skidding. He does so by banking the road in such a way that the force causing the centripetal acceleration will be supplied by the component of the normal force toward the center of the path
a. Show that for a given speed v and radius r the curve must be banked at an angle \Theta such that tan\Theta = v^2/r * g
a_c (centripetal acceleration) = V^2 / r
\SigmaF_y = m * a = 0
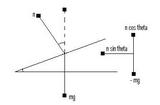
i hope this diag. makes sense to you...
According to the question a_c = n * Sin\Theta ---- (1)
Then
\SigmaF_y = m * a = 0
(n * Cos \Theta) - (m * g) = 0
n = (m * g) / (Cos \Theta) -------- (2)
substitute 2 in 1 for n
a_c = (m * g) / (Cos \Theta) * Sin\Theta
= (m * g) Tan \Theta
now a_c (centripetal acceleration) = V^2 / r
therefore (V^2 / r) = (m * g) Tan \Theta
and Tan \Theta = (V^2) /(m * g * r)
what am i doing wrong ?.?
Homework Statement
An Engineer wishes to design a curved exit ramp for a toll road in such a way that a car will not have to rely on friction to round the curve without skidding. He does so by banking the road in such a way that the force causing the centripetal acceleration will be supplied by the component of the normal force toward the center of the path
a. Show that for a given speed v and radius r the curve must be banked at an angle \Theta such that tan\Theta = v^2/r * g
Homework Equations
a_c (centripetal acceleration) = V^2 / r
\SigmaF_y = m * a = 0
The Attempt at a Solution
i hope this diag. makes sense to you...
According to the question a_c = n * Sin\Theta ---- (1)
Then
\SigmaF_y = m * a = 0
(n * Cos \Theta) - (m * g) = 0
n = (m * g) / (Cos \Theta) -------- (2)
substitute 2 in 1 for n
a_c = (m * g) / (Cos \Theta) * Sin\Theta
= (m * g) Tan \Theta
now a_c (centripetal acceleration) = V^2 / r
therefore (V^2 / r) = (m * g) Tan \Theta
and Tan \Theta = (V^2) /(m * g * r)
what am i doing wrong ?.?