Change in Pressure: Find Gas P (Pa) Experiment

[Devin Longo]

Homework Statement

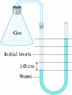
An experiment to determine the specific heat of a gas makes use of a water manometer attached to a flask (the figure below ). Initially the two columns of water are even. Atmospheric pressure is 1.5 105 Pa. After heating the gas, the water levels change to those shown. Find the change in pressure of the gas in Pa.



2. Homework Equations
$$\Delta$$P = $$\rho$$g$$\Delta$$h

The Attempt at a Solution

I basically did 1.5 x 10 ^5 * 9.8 m/s2 * .01m (what I assume given the picture to be the change in height)

 

[rl.bhat]

Difference in water level is 4 cm.
So ΔP = ρgΔh.

 

[Devin Longo]

If I change 4 cm to meters I get 58800 as the calculated total from the equation, which is incorrect according to the website. Is there some factor I'm neglecting?

 

[cepheid]

If I change 4 cm to meters I get 58800 as the calculated total from the equation, which is incorrect according to the website. Is there some factor I'm neglecting?

Rho is the density of the fluid, not the pressure, so I'm not sure why you are using 1.5e5 in the equation. Also, pay attention to units when you are doing your computation (doing so would have revealed this error).