Change of variable in an integral

[Bestfrog]

Homework Statement

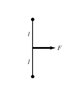
A massless string of length 2l connects two hockey pucks that lie on frictionless ice. Aconstant horizontal force F is applied to the midpoint of the string, perpendicular to it (see right figure). How much kinetic energy is lost when the pucks collide, assuming they stick together?

The Attempt at a Solution

Putting a y-axis along the string when it is straight and a x-axis along the direction of the force, the force acting on the puck "at the bottom" along the t-axis is $\frac{F}{2}\cdot tan \theta$.
So, by calculating the work for this puck I obtain $W=\int_{-l}^{0} \frac{F\cdot tan \theta}{2}dy=\int_{-l}{0} \frac{F\cdot tan \theta}{2} d(l\cdot sin\theta)= \int_{\frac{-\pi}{2}}^{0} \frac{Fl}{2}\cdot sin\theta d\theta$.
Can you explaine me how the last passage works?

 

[phyzguy]

It's a change of variables y = l \sin(\theta).

Since l is constant: d(l \sin(\theta)) = l d(\sin(\theta)) = l \cos(\theta) d \theta.

So: \frac{F \tan(\theta)}{2}d(l \sin(\theta)) = \frac{F l \tan(\theta) \cos(\theta)}{2}d \theta = \frac{F l \sin(\theta)}{2}d \theta.

Then since y = l \sin(\theta), you need to change the integration limit from y = -l to \theta = \frac{-\pi}{2}.

Does this answer your question?

 

[Bestfrog]

Does this answer your question?

Perfectly, thank you!