Change of Variables: Integral of x^2+y^2 in Region B

[rocket]

Hi,
I'm not sure how to do this question. Any help would be great.

Let B be the region in the first quadrant of R^2 bounded by xy=1, xy=3, x^2-y^2=1, x^2-y^2=4. Find \int_B(x^2+y^2) using the substitution u=x^2-y^2, v=xy.. Use the Inverse Function theorem rather than solving for x and y explicitly.

 

[Pyrrhus]

what have you done? did you calculate the jacobian?

 

[saltydog]

Hi,
I'm not sure how to do this question. Any help would be great.

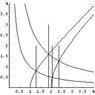
Let B be the region in the first quadrant of R^2 bounded by xy=1, xy=3, x^2-y^2=1, x^2-y^2=4. Find \int_B(x^2+y^2) using the substitution u=x^2-y^2, v=xy.. Use the Inverse Function theorem rather than solving for x and y explicitly.

Hello Rocket. Welcome to PF. You know, I've been working with the Implicit Function Theorem lately too and feel this problem nicely accentuates my work. This is what I think and I hope those in here better than me will correct anything I say that reflects my recent understanding of the theorems.

The problem here is two fold: Calculating the correct Jacobian and then figuring out what are the new limits of integration in terms of u and v. Have you looked at the theorem and especially the case when the transformation is from \mathbb{R}^2\rightarrow\mathbb{R}^2? That's the case above since we have (x,y) to (u,v). In this case, the Implicit Function Theorem reduces to the Inverse Function Theorem which under suitable restrictions, (Jacobian not zero), guarantees the existence of an inverse function. If we have an inverse function, then we have one-to-one and thus:

In the case above we have:

f:(x,y)\rightarrow (x^2-y^2,xy)

In order to solve the indicated integral by change of variable, we require the inverse functions:

x=h(u,v)

y=k(u,v)

and the Jacobian:

\frac{\partial(x,y)}{\partial(u,v)}

However, if the transformations above satisfy the requirements of the Implicit Function Theorem, i.e., are one-to-one in the requested domain, we can solve for this Jacobian using the following relationship:

\frac{\partial(x,y)}{\partial(u,v)}=\frac{1}{\frac{\partial(u,v)}{\partial(x,y)}}

Now, how do we figure out the new bounds on the integral? How about substituting the values of u and v into the four equations?

 

[saltydog]

Rocket, where you at with this anyway? Can you break it up into three regular double integrals, work it out and then compare the results with the results obtained via change of variables? You like doin' extra work? Big negatory? Anyway, I have a slight problem with the Inverse Function Theorem and the substitution:

f(h(u,v),k(u,v)))

that's needed to do the integration. I interpret this, from the IFT, to be equivalent to f(x,y) and work accordingly but I'm a bit unsure. Seems to work (agrees with the three integrals above), but still I've never done one of these from the perspective of the Inverse Function Theorem. Hopefully we'll get some more replys and we can both learn from them.

Edit: Oh yea, here's the plot and the intervals for the 3 doubles if you're interested. You can calculate those 4 points right?

 

[OlderDan]

Rocket, where you at with this anyway? Can you break it up into three regular double integrals, work it out and then compare the results with the results obtained via change of variables? You like doin' extra work? Big negatory? Anyway, I have a slight problem with the Inverse Function Theorem and the substitution:

f(h(u,v),k(u,v)))

that's needed to do the integration. I interpret this, from the IFT, to be equivalent to f(x,y) and work accordingly but I'm a bit unsure. Seems to work (agrees with the three integrals above), but still I've never done one of these from the perspective of the Inverse Function Theorem. Hopefully we'll get some more replys and we can both learn from them.

Edit: Oh yea, here's the plot and the intervals for the 3 doubles if you're interested. You can calculate those 4 points right?

What are you unsure about? The 3 double integrals you talk about add up to 3 by my calculation (using the services of http://www.quickmath.com ). Using the Inverse Function Theorem as you posted it leads to a constant function integrated over the variables u and v, which were chosen to make all the integration limits constant; the integral becomes a constant times the area of a rectangle and yields consistent results.

 

[saltydog]

Hello Dan, This is what:

Letting:

T:\mathbb{R}^2\rightarrow\mathbb{R}^2\quad\text{where:}

T(x,y)=(x^2-y^2,xy)=(u(x,y),v(x,y))

We find:

\int_B F(x,y)dxdy=\int_A F[h(u,v),g(u,v)]\frac{\partial(x,y)}{\partial(u,v)}dudv

with:

x=h(u,v)

y=g(u,v)

However, we do not determine h(u,v) and g(u,v) directly and so I'm left with the integral:

\int_A (x^2+y^2) \frac{1}{2(x^2+y^2)} dudv


It's the substituting of F(x,y) for F[h(u,v),g(u,v)] and the awkwardness of having x,y and u and v in the same integral. What am I doing wrong?

 

[krab]

\int_A (x^2+y^2) \frac{1}{2(x^2+y^2)} dudv


It's the substituting of F(x,y) for F[h(u,v),g(u,v)] and the awkwardness of having x,y and u and v in the same integral. What am I doing wrong?

Ummm. Don't the x^2+y^2 cancel, leaving no x and y dependence in the integrand?

 

[saltydog]

Ummm. Don't the x^2+y^2 cancel, leaving no x and y dependence in the integrand?

Yes, yes, I know that Krab. And I remember you helping me with Hurkyl's tricky integral some time ago too. Thanks. With regards to the above, just the fact that they're there and I have to use expressions in terms of x and y is what I find a bit awkward. I realize the best way out of this is to work 10 or 12 more. Perhaps I should look at a few more anyway.

 

[saltydog]

Ok, I have a good question: Suppose they wouldn't cancel. Suppose we had this:

\int_A (x^2+y^3) \frac{1}{2(x^2+y^2)} dudv

Then what? Would we then be reduced to finding explicit expressions for x and y in terms of u and v I suppose?

Suppose we couldn't find explicit expressions? Could we still rely on the Inverse Function Theorem to solve the problem?

Rocket, where you at anyway? Hope I didn't run you off by asking you to do those extra 3 integrals. Just a suggestion you know.

 

[OlderDan]

Ok, I have a good question: Suppose they wouldn't cancel. Suppose we had this:

\int_A (x^2+y^3) \frac{1}{2(x^2+y^2)} dudv

Then what? Would we then be reduced to finding explicit expressions for x and y in terms of u and v I suppose?

Suppose we couldn't find explicit expressions? Could we still rely on the Inverse Function Theorem to solve the problem?

If the x,y dependence did not divide out, you would have to find x(u,v) and y(u,v) in order to perform the integral over u,v. The theorem would still apply as long as the one-to-one condition was satisfied, but it would not be as useful as in the original problem.