JD_PM
- 1,125
- 156
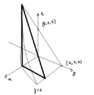
Homework Statement
$$\int_{-23/4}^4\int_0^{4-y}\int_0^{\sqrt{4y+23}} f(x,y,z) dxdzdy$$
Change the order of the integral to
$$\iiint f(x,y,z) \, \mathrm{dydzdx}$$What I have done
It is just about:
From ##x=0## to ##x=\sqrt{4y+23}##
From ##z=0## to ##z=4-y##
From ##y=\frac{x^2-23}{4}## to ##y=4##
So
$$\int_0^{\sqrt{23}}\int_0^4\int_{\frac{x^2-23}{4}}^{4} f(x,y,z) dydzdx$$
But this is incorrect. What am I missing?
Thanks
Last edited by a moderator: