Supernats
- 18
- 0
[SOLVED] Charge moving through electric and magnetic field
I'm pretty sure my answer for part (a) was correct, but I'll include it just for kicks. Also, I'm sorry if it's wordy, this is my first post and not exactly sure what protocol is, so I'm just copying from the book.
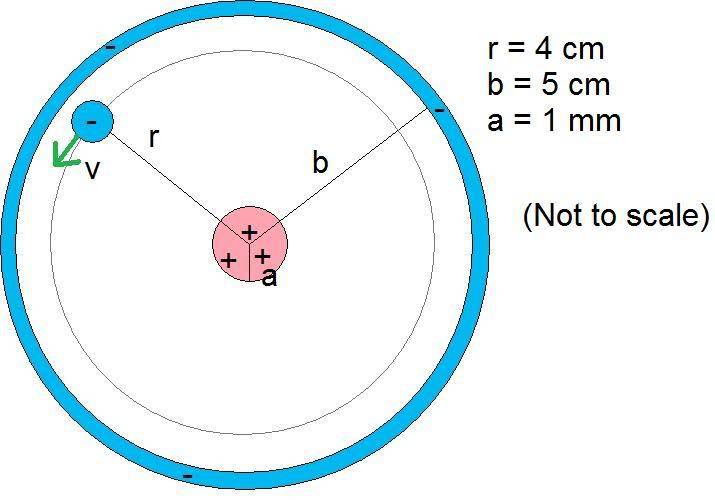
An electron moves in a circular path with radius r=4.00 cm in the space between two concentric cylinders. The inner cylinder is a positively charged wire with radius a = 1.00 mm and the outer cylinder is a negatively charge hollow cylinder with radius b = 5.00 cm. The potential difference between the inner and outer cylinders is V_a_b = 120 V, with the wire being at the higher potential. The electric field in the region between the cylinders is radially outward and has magnitude E = \frac{V_a_b}{r \ln(\frac{b}{a})}.
a) Determine the speed the electron needs to maintain its circular orbit. You can ignore bother the gravitational and magnetic fields of the earth.
b) Now include the effect of the Earth's magnetic field. If the axis of symmetry of the cylinders is positioned parallel to the magnetic field of the earth, at what speed must the electron move to maintain the same circular orbit? Assume that the magnetic field of the Earth has magnitude 1.30 X 10^-4 T and that its direction is out of the plane of the page in the figure.
For part (a), I used \sum F = m a, giving me q E = \frac{m v^2}{r}, which becomes v = \sqrt{\frac{r q E}{m}}. This gave me 5.39 x 10^12 m/s.
For part (b).
F_b = q v \times B.
Obviously Newton's second law will come into play again, so \sum F = F_B + F_E = q(E + v \times B = m a = \frac{m v^2}{r}.
I'm basically stumped here. I tried \frac{m v^2}{r} = q v B + q E with the quadratic formula but I'm getting a negative discriminant. Dimensional analysis works out, but my numbers don't. (I just put e in for q since we're talking about an electron.)
I got v = \frac{r(-e B \pm \sqrt{B^2 e^2 - 4 \frac{m e E}{r}}}{2m}.
Homework Statement
I'm pretty sure my answer for part (a) was correct, but I'll include it just for kicks. Also, I'm sorry if it's wordy, this is my first post and not exactly sure what protocol is, so I'm just copying from the book.
An electron moves in a circular path with radius r=4.00 cm in the space between two concentric cylinders. The inner cylinder is a positively charged wire with radius a = 1.00 mm and the outer cylinder is a negatively charge hollow cylinder with radius b = 5.00 cm. The potential difference between the inner and outer cylinders is V_a_b = 120 V, with the wire being at the higher potential. The electric field in the region between the cylinders is radially outward and has magnitude E = \frac{V_a_b}{r \ln(\frac{b}{a})}.
a) Determine the speed the electron needs to maintain its circular orbit. You can ignore bother the gravitational and magnetic fields of the earth.
b) Now include the effect of the Earth's magnetic field. If the axis of symmetry of the cylinders is positioned parallel to the magnetic field of the earth, at what speed must the electron move to maintain the same circular orbit? Assume that the magnetic field of the Earth has magnitude 1.30 X 10^-4 T and that its direction is out of the plane of the page in the figure.
Homework Equations
For part (a), I used \sum F = m a, giving me q E = \frac{m v^2}{r}, which becomes v = \sqrt{\frac{r q E}{m}}. This gave me 5.39 x 10^12 m/s.
For part (b).
F_b = q v \times B.
Obviously Newton's second law will come into play again, so \sum F = F_B + F_E = q(E + v \times B = m a = \frac{m v^2}{r}.
The Attempt at a Solution
I'm basically stumped here. I tried \frac{m v^2}{r} = q v B + q E with the quadratic formula but I'm getting a negative discriminant. Dimensional analysis works out, but my numbers don't. (I just put e in for q since we're talking about an electron.)
I got v = \frac{r(-e B \pm \sqrt{B^2 e^2 - 4 \frac{m e E}{r}}}{2m}.
Attachments
Last edited: