Charge on Capacitor in Pure Capacitance Circuit?

[eprparadox]

Homework Statement

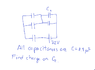
I apologize for having to upload an attachment but I couldn't describe this circuit. Basically, there is set of capacitors and the question is asking for the charge on one of them, when a 72 volt source is attached. All capacitances are 8.9 microFarads.

Homework Equations

Q = C*V

The Attempt at a Solution

I believe the top two pairs of capacitors are in parallel. So if we simplify those, then we end up with 3 capacitors in series, one of which is 8.9 microF, and the other two that are 17.8 microF.

Then from there, I can say the charge on all 3 capacitors is going to be the same (since they're in series) and so if I combine all 3 of these capacitors in series, I get 4.45 microF equivalent capacitange.

And if I have a 72 volt source, then I get Q = Ceq*V = 320 microC. So then the voltage across the parallel combination (which is 17.9 microF) becomes V = 320 microC / 17.9 microF = 17.9 V. This is the same voltage that is across the original C2 capacitor so the final charge on C2 should work out to be Q = C * V = 8.9 microF * 17.9 V = 159 microCoulombs as my Final answer.

I hope that makes sense. I just want to know if my mindset is correct in working through this.

Any help from you guys and girls is greatly appreciated.

 

[willem2]

This is entirely correct. I would do all the computations with C and V, only substituting numbers for the final answer.

 

[Adjuster]

There is also a simpler way of approaching this problem - I was tempted to post the whole method, but worried about getting in trouble for giving a direct answer.

Suffice it to say that four identical capacitors connected as two groups in series, each of two capacitors in parallel equals...what exactly?

This should lead rapidly on to finding what fraction of the supply voltage falls across C2. It's a simple fraction, giving a voltage very close to your value of 17.9V.

I would agree with willem2 that you should try to leave calculations to the end. Although your working is basically correct there seems to be a very small arithmetic error.