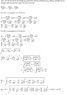Charge on q from other charges given net force is zero

[Physics2341313]

Homework Statement

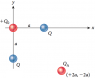
Consider the figure below, we need to find the charge on Q_0, both charges Q are negative. It is given that the net charge on Q_A is zero.

The figure of the problem is attached.

The Attempt at a Solution

I understand how to get the solution except for one part. I'm just going to write F_x and F_y below to denote the forces components as the numbers aren't relevant (I don't think?) for my question.

I understand that we can discard the constant 1/4\pi\epsilon_0 or k whichever is preferred and that we can get rid of the a^2 terms in denominators when taking the radius and likewise for sin/cos for the respective components.

The solution is Q_0 Q/8 = \sqrt {F_x^2 + F_y^2}.

Now the solution is obtained by Q_0 = 8 * \sqrt {F_x^2 + F_y^2}

Why is Q discarded here? I just don't see where it goes mathematically.. it just kind of "disappears". Is it discarded because it is stated that the net force caused by this charge is negligible?

 

[haruspex]

It is given that the net charge on QA is zero.

That doesn't mean anything. Do you mean the net force on Q_A is zero, or the potential at Q_A is zero?

Please clarify what F_x and F_y represent.
I don't understand why you would have Q₀Q in an equation. You don't care about any forces acting between Q₀ and the two Q charges. Did you mean Q₀Q_A?

 

[thepatient]

The units on the solution aren't consistent. They show that (units of electric charge)^2 = force.

 

[Physics2341313]

I didnt understand where the Q went until I reworked it and yes you're right. Is the below correct? It gives me the correct answer but as far as best way to solve technique etc goes not sure its close to good.

My notation could probably use some work... I realize I could have forgotten about the Q_0 components but split this up for practice breaking components up anyways.

I attached the work instead of trying to type tons of latex and mess it up

 

[haruspex]

I didnt understand where the Q went until I reworked it and yes you're right. Is the below correct? It gives me the correct answer but as far as best way to solve technique etc goes not sure its close to good.

My notation could probably use some work... I realize I could have forgotten about the Q_0 components but split this up for practice breaking components up anyways.

I attached the work instead of trying to type tons of latex and mess it up

It's probably neater to use the symmetry. Just use the components parallel to the line x+y=0.

 

[Physics2341313]

I'm not sure what you mean? I'm very bad at using symmetry doing these types of problems typically takes me ages as I can't identify the symmetry / relations correctly in square arrays of charge etc. Could you explain what you mean?

 

[haruspex]

I'm not sure what you mean? I'm very bad at using symmetry doing these types of problems typically takes me ages as I can't identify the symmetry / relations correctly in square arrays of charge etc. Could you explain what you mean?

Where could you put a straight line through the diagram so that the portions on eithe side are mirror images of each other? Hint: two of the charges are unique, so it must pass through each of those.