Charges mass on the end of a light string

[MissPenguins]

Homework Statement

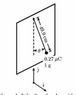
A charged mass on the end of a light string is
attached to a point on a uniformly charged
vertical sheet (with areal charge density
0.25 μC/m²) of infinite extent.

Look at attachment for diagram
Find the angle $\theta$ the thread makes with the
vertically charged sheet. The acceleration of
gravity is 9.8 m/s² and the permittivity of free
space is 8.854 × 10⁻¹² C²/N · m² .
Answer in units of degree.
I got the first part right to be 21.254189 using $\theta$=tan^-1(qE/mg)
I need help with part 2
Find $\sigma$ for an angle of 77^o .
Answer in units of μC/m².

Homework Equations

$\theta$=tan^-1(qE/mg)
qE = $\sigma$/2E_o

The Attempt at a Solution

Since $\theta$=tan^-1(qE/mg), so I did tan(77^o) = (qE)(mg)
qE = 0.0038118 (calculated from part 1)
mg = 0.0098
$\sigma$=(qE)(mg) = 7.51677X10^-13
Converted back to uC = 7.51677X10^-7

What did I do wrong? Thank you!

 

[Redbelly98]

E will be different for part 2, since the charge density is different.

Also, did you mean (qE)/(mg) instead of (qE)(mg)?

 

[MissPenguins]

E will be different for part 2, since the charge density is different.

Also, did you mean (qE)/(mg) instead of (qE)(mg)?

Yea. tan(77) = (qE/mg) which is qE=mgtan(77) = 0.04244
I am not sure what other charge density do I have to use. E₀is a constant, that's given.
PLEASE HELP!

Same question as this one https://www.physicsforums.com/showthread.php?t=109643
Except part 2 was not explained.

 

[Redbelly98]

Okay, found another mistake:

qE = $\sigma$/2E_o

Actually, it's E = $\sigma$/2e_o (no q here).

Does that help?

 

[MissPenguins]

Okay, found another mistake:

Actually, it's E = $\sigma$/2e_o (no q here).

Does that help?

The previous one wasn't a mistake.
It's qE = mgtan(77) = 0.042448
I already did this $\sigma$ = (E)(2E_o).
So (0.042448)(2(8.85X10^-12) = 7.5133X10^-13. I converted back to uC = 7.51633X10^-7. And it is wrong! :(

 

[Redbelly98]

The previous one wasn't a mistake.
It's qE = mgtan(77) = 0.042448

I agree, qE = 0.042448 N.

So based on that, what is E equal to?

I already did this $\sigma$ = (E)(2E_o).
So (0.042448)(2(8.85X10^-12) = 7.5133X10^-13.

Okay. But E is not 0.042448 -- see my comment above.

 

[MissPenguins]

I agree, qE = 0.042448 N.

So based on that, what is E equal to?


Okay. But E is not 0.042448 -- see my comment above.

You said E is different for part 2 since the charge density changed. So how do I find E? I attempted to do (0.25E-6)/(2*8.854E-12) = 14117.91281 for E, is this right for E?
Then use (14117.91281)(2*8.854E-12) = 2.5E-7?
It doesn't make sense. Can you give me more hints? Thanks.

 

[gneill]

You've already written an equation of the form

tan(θ) = (q*E)/(m*g)

Can you not rearrange to find E? With E can you find σ ?

 

[MissPenguins]

I figured the problem out. Thank you very much everyone!