Chemistry Help - Using the Gas Laws

AI Thread Summary
The discussion revolves around calculating the final pressure of an ideal gas when its temperature is increased from 20.0 degrees Celsius to 200.0 degrees Celsius, while keeping the volume constant at 1.00 L. The relevant gas law for this scenario is Guy-Lussac's Law, which relates pressure and temperature. The initial conditions are 1.00 atm and 20.0 degrees Celsius, and the final temperature is 200.0 degrees Celsius. By applying Guy-Lussac's Law, the final pressure can be determined based on the temperature change. This calculation is essential for understanding gas behavior under constant volume conditions.
sam.
Messages
16
Reaction score
0

Homework Statement



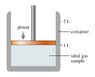
This figure (file attached) shows a container that is sealed at the top by a movable piston. Inside the container is a ideal gas at 1.00 atm, 20.0 degrees Celsius, and 1.00 L.

The gas sample has now returned to its original state of 1.00 atm, 20.0 degrees Celsius and 1.00 L. What will the pressure become if the temperature of the gas is raised to 200.0degrees celsius and the piston is not allowed to move?

Homework Equations



Boyle's Law P_1V_1 = P_2V_2
or
Charles' Law V_1/T_1 = V_2/T_2

The Attempt at a Solution



Okay, in order for the piston not to move, this means that the volume must remain at 1.00 L. What I don't know what to do is how to relate temperature and pressure to solve for the final pressure.
 

Attachments

  • Chem pic.jpg
    Chem pic.jpg
    5.8 KB · Views: 489
Physics news on Phys.org
Guy-Lussacs Law P1/T1 = P2/T2
 
Thread 'Confusion regarding a chemical kinetics problem'

Thread 'Confusion regarding a chemical kinetics problem'

TL;DR Summary: cannot find out error in solution proposed. [![question with rate laws][1]][1] Now the rate law for the reaction (i.e reaction rate) can be written as: $$ R= k[N_2O_5] $$ my main question is, WHAT is this reaction equal to? what I mean here is, whether $$k[N_2O_5]= -d[N_2O_5]/dt$$ or is it $$k[N_2O_5]= -1/2 \frac{d}{dt} [N_2O_5] $$ ? The latter seems to be more apt, as the reaction rate must be -1/2 (disappearance rate of N2O5), which adheres to the stoichiometry of the...
View full post »

Similar threads

Chemistry To determine variables in adiabatic reversible process do we need to look up heat capacity?
Replies
1
Views
2K
Chemistry Calculation of thermodynamic variables for irreversible adiabatic process of ideal gas
Replies
9
Views
2K
Chemistry How to explain the difference between recompression of ideal gas reversibly and irreversibly after initial irreversible expansion?
Replies
5
Views
2K
Chemistry A few questions on an irreversible adiabatic expansion of an ideal gas
Replies
1
Views
2K
Solubility of gas using Henry's law
Replies
2
Views
2K
Calculating ΔE Difference for 2 Samples of Monatomic Ideal Gas
Replies
4
Views
2K
Thermodynamics: Compression of an Adiabatic Gas
Replies
2
Views
2K
How Much Magnesium is Needed for 40 mL of Hydrogen Gas Production?
Replies
2
Views
7K
Solve a Gas Law Problem: Find T in °C
Replies
7
Views
2K
Ideal Gas Law Gas in a Piston Problem
Replies
1
Views
4K

Hot Threads

Recent Insights

Back
Top