vadevalor
- 35
- 0
Circuit -- Why a more accurate value of the resistance?
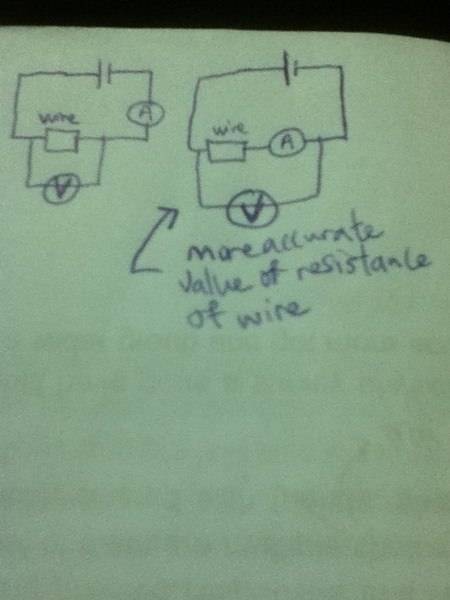
Note: CURRENT CAN FLOW THROUGH THE VOLTMETER IN THESE CASES.
Why does the second setup as shown by the arrow in the picture give a more accurate value of the resistance of that wire?
It says the current in setup 1 on the left measured by the ammeter includes both the current through the wire and current through the voltmeter,
but for setup 2 on the right, it says this setup the ammeter will measure the current in the wire only.
They are both series circuits, so i can't get why there is a difference in currents for the 2?
Note: CURRENT CAN FLOW THROUGH THE VOLTMETER IN THESE CASES.
Why does the second setup as shown by the arrow in the picture give a more accurate value of the resistance of that wire?
It says the current in setup 1 on the left measured by the ammeter includes both the current through the wire and current through the voltmeter,
but for setup 2 on the right, it says this setup the ammeter will measure the current in the wire only.
They are both series circuits, so i can't get why there is a difference in currents for the 2?