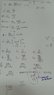- #1
Anon.ilbe
- 7
- 0
Homework Statement
http://www.webassign.net/hrw/W0490-N.jpg
The figure above shows three circular arcs centered on the origin of a coordinate system. On each arc, the uniformly distributed charge is given in terms of Q= 2*10-6C. The radii are given in terms of R = 10cm. What is the magnitude of the net electric field at the origin due to the arcs?
Homework Equations
dE = Kλds / r2
ds=rdθ
λ= Charge / Length ⇒ Q/2πr ⇒ Q/(2πr/4) - since only quarter is shown ⇒ 2Q/(πr)
The Attempt at a Solution
So i think I got all the steps correct except i can't figure out why i have to multiply sin(45) to get to the right answer at the end.
1. dE = Kλds / r2 - used this formula b/c it's a ring
2. dEcosθ = Kλds / r2 (cosθ) - multiplied cosθ b/c perpendicular component (sinθ) cancels each other.
3. dEcosθ = Kλrdθ / r2 (cosθ) - replaced ds to rdθ b/c cosθ is present and thus want to integrate along 90° to 180°
4. ∫dEcosθ = ∫Kλrdθ / r2 (cosθ) ⇒ E = Kλ/r ∫(cosθ)dθ - r on the numerator and r2 on the denominator cancels to make denominator just r. since r is constant, took out of the integral and just integrate cosθdθ from 90° to 180°
5. E = Kλ/r [-sin(180°)-(-sin(90°)] ⇒ E = Kλ/r - integral just turns out to be 1 and we are left with E = Kλ/r
6. E = Kλ/r - This is 1st arc so to second and third, we just replace r with 2r and 3r respectively. Then we get
E1 = Kλ/r ; E2 = Kλ/2r ; E3 = Kλ/3r
7. Replace λ with 2Q/πr (relevant equation section)
E1 = K(2Q/πr)/r ; E2 = K(2Q/πr)/2r ; E3 = K(2Q/πr)/3r
E1 = K(2Q/πr2) ; E2 = K(Q/πr2) ; E3 = K(2Q/3πr2)
8. Replace Q and r with respective charge and radius
E1 = K(2Q/π(R)2) ; E2 = K(-4Q/π(2R)2) ; E3 = K(18Q/3π(3R)2)
E1 = K(2Q/π(R)2) ; E2 = K(-4Q/π4R2) ; E3 = K(6Q/π(9R2)
9. Simplify
E1 = K(2Q/π(R)2) ; E2 = K(-Q/πR2) ; E3 = K(2Q/π(3R2)
E1 = K(6Q/π3(R)2) ; E2 = K(-3Q/π3R2) ; E3 = K(2Q/π(3R2)
※Multiplied E1 and E2 by 3 on both numerator and denominator to simplify
E1 + E2 + E3 = Enet
Enet = K5Q/π3(R)2
--------------------------------------------------------
crap... i don't know where I messed up.
Originally i got E1 = 2Q/4πr2ε0 + E2 = -4Q/4πr2ε0 + E3 = 6Q/4πr2ε0
Which turned out to be
Enet = Q/π2r2ε0
which turned out to be 228974
but the answer is 161903 which is just sin(45) multiplied by 228974.
why do you need to multiply sin45?
Last edited: