Genericcoder
- 130
- 0
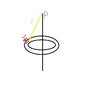
Suppose you want to find the magnetic field at a point p at the z axis from the picture attached.
Attempt to understand this problem:
The way the books solves it is that it says the angle theta between current element i ds and r is 90.
Then he calculates the integeral which has two parts DB perpendicular and DB parrallel to z axis.
But now that's my issue didn't we already say that i ds and r is 90 degree with respect to each other?? why do we need now to calculate DB parrallel to z-axis I understand how he did that calculation or why he did this calculation but what I don't understand why did mention at first that ds and r are perpindicular if that's the case wouldn't the answer be only dB = (u0i / 4PI) *( ds /r^2)
and we didn't need to do anything with the integeral?
I am hoping to understand this coz this thing about r ds being perpinduclar doesn't make sense to me.
Attempt to understand this problem:
The way the books solves it is that it says the angle theta between current element i ds and r is 90.
Then he calculates the integeral which has two parts DB perpendicular and DB parrallel to z axis.
But now that's my issue didn't we already say that i ds and r is 90 degree with respect to each other?? why do we need now to calculate DB parrallel to z-axis I understand how he did that calculation or why he did this calculation but what I don't understand why did mention at first that ds and r are perpindicular if that's the case wouldn't the answer be only dB = (u0i / 4PI) *( ds /r^2)
and we didn't need to do anything with the integeral?
I am hoping to understand this coz this thing about r ds being perpinduclar doesn't make sense to me.