Circular Motion With Constant Angular Acceleration

[Hoophy]

Homework Statement

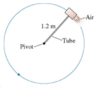
Question: A 600 g steel block rotates on a steel table while attached to a 1.20 m-long hollow tube. Compressed air fed through the tube and ejected from a nozzle on the back of the block exerts a thrust force of 5.01 N perpendicular to the tube. The maximum tension the tube can withstand without breaking is 40.0 N. Assume the coefficient of kinetic friction between steel block and steel table is 0.60.
If the block starts from rest, how many revolutions does it make before the tube breaks?

Homework Equations

My variables and constants:
Steel Block Mass = m = 0.600 kg
Radius = r = 1.2 m
Maximum Tension = T = 40.0 N
Thrust/Tangential Force = F = 5.01 N
g = 9.8 m/s²
Weight = mg
Coefficient of Kinetic Friction = μ = 0.60
Normal Force = N
Friction = z
Centripetal Acceleration = a_c
Angular Acceleration = α
Maximum Angular Velocity = ω
Maximum Tangential Velocity = v
Tangential Acceleration = a_t

The Attempt at a Solution

a) I drew a partial free body diagram showing only the vertically acting forces Normal Force (up, positive y) and Weight (down, negative y)
b) I summed the forces in the vertical axis:
F_vertical: 0 = N - mg
c) I isolated N:
N = mg
d) I drew another partial free body diagram showing only Friction (z), Thrust, and Tension. The situation I used is one in which the Steel Block is directly North of the center-point of the circular path such that Tension points South, Thrust points West, and Friction points East.
I defined my coordinate system as:
1) Positive x is West
2) Positive y is South
e) I summed the forces in the y axis:
F_y: ma_c = T
a_c = T/m
f) I summed the forces in the x axis:
F_x: ma_t = F - z
ma_t = F - μmg
a_t = (F/m) - μg
g) I did circular motion shenanigans:
a_c = v²/r = T/m
See (e)
v = sqrt(Tr/m)
ω = v/r
ω = ( sqrt(Tr/m) )/r = ( sqrt[ (40)(1.2)/(0.6) ] )/(1.2) = 7.45356 rad/s
α = a_t/r
See (f)
α = ( (F/m) - μg )/r = F/(mr) - (μg)/r = (5.01)/( (0.600)(1.2) ) - (0.60)(9.8)/(1.2) = 2.05833 rad/s²
h) More circular motion shenanigans:
Kinematic Equation: ω² = 2αΔθ
Δθ = ω²/(2α) = (7.45356)²/(2(2.05833)) = 13.4953 rad
i) I computed the number of revolutions:
Δθ/2π = (13.4953)/2π = 2.1478 revs = 2.1 revs

4. A note
2.1 revs is not the correct answer, nor is 2.1478 revs. Also I do not know what the correct answer is...
I don't know where I went wrong.
Thanks for taking the time to read this!

[EDIT] 2.1 revolutions is correct.

 

[haruspex]

2.1 revs is not the correct answer, nor is 2.1478 revs.

Using your analysis I get the same answer, but I wonder if we need to consider the flow of air in the tube. As that flows out from the centre it gains tangential velocity, and the work for that comes from the thrust.

 

[Hoophy]

Using your analysis I get the same answer, but I wonder if we need to consider the flow of air in the tube. As that flows out from the centre it gains tangential velocity, and the work for that comes from the thrust.

My class has not progressed that far yet (I don't even know if this is within the scope of that class) so I doubt they would expect us to model this. Of course, you had no way of knowing that.

I just checked again, apparently my calculated answer is correct and I simply typed in the wrong number for my submission...
...I guess I'll mark this question as solved.

Thank you for responding!

 

[haruspex]

My class has not progressed that far yet (I don't even know if this is within the scope of that class) so I doubt they would expect us to model this. Of course, you had no way of knowing that.

I just checked again, apparently my calculated answer is correct and I simply typed in the wrong number for my submission...
...I guess I'll mark this question as solved.

Thank you for responding!

Very good.
My thought doesn't help anyway. We would need more information about the flow. E,g. by making the air at very high pressure the pipe could be kept very thin, so hardly any air mass.