Classical Mechanics - Find angular velocity of two rods

[Mikkel]

Homework Statement

Hello!
I apologize for my poor setup, first post.
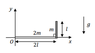
I am given a system of two rods, hope you can see my image.http://file:///C:/Users/Mikkel/Downloads/Mek2_exam_Jan2016_final.pdf
One along the x-axis with mass = 2m and length = 2l
Another perpendicular with the other with mass = m and length = l

The system rotate around a point O

Find the angular velocity at the point when the systems longest rod is vertical.

Homework Equations

I have calculated the center of mass rcm = ( (4/3)*l , (1/6)*l )

and the distance from pivot point to the center of mass = (1/6) * sqrt(65) * l

Also the moment of inertia for the system = 7*m*l²

The Attempt at a Solution

I have tried the following so far:

I tried to use conservation of energy to solve it:

m*g*h + 0 = 0 + (1/2)*I*w²

I am thinking that I have a total of mass 3
and the height has to be the x-coordinate for center of mass (I think this is where I might be wrong?)

3*m*g*(4/3)*l = (1/2)*7*m*l² * ω²

after a bit of calculations...

ω = sqrt((8*g)/(7*l))

However my facit says ω = sqrt((9*g)/(7*l))

I can't figure it out!

Appreciate any tips ! :)

 

[haruspex]

3*m*g*(4/3)*l = (1/2)*7*m*l2 * ω2

You have omitted a contribution to the change in height of the mass centre.

 

[Mikkel]

You have omitted a contribution to the change in height of the mass centre.

Hmm I don't see how. I was thinking that, when the rod is vertical the height is zero.

 

[TSny]

Draw a diagram and mark the location of the center of mass at the initial and final positions.

 

[Mikkel]

Draw a diagram and mark the location of the center of mass at the initial and final positions.

Ah you are a god damn genius sir!

So the center of mass changes to (3/4) * l when it is vertical and then it becomes (9g/7l)
Thank you!

 

[haruspex]

It is rather simpler if you do not bother finding the mass centre of the L shape. Just work out and sum the two moments of inertia, and likewise the two changes in PE.