Saitama
- 4,244
- 93
Homework Statement
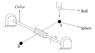
The given figure shows a mechanical system free of any dissipation. The two spheres (A and B) are each of equal mass m, and a uniform connecting rod AB of length 2r has mass 4m. The collar is massless. Right above the position of sphere A in figure is a tunnel from which balls each of mass m fall vertically at suitable intervals. The falling ballscause the rods and attached spheres to rotate. Sphere B when it reaches the position now occupied by sphere A, suffers a collision from another falling ball and so on. Just before striking, the falling ball has velocity v. All collisions are elastic and the spheres as well as the falling balls can be considered to be point masses. (Attachment 1)
(a) Find the angular velocity ##\omega_{i+1}## of the assembly in terms of {##\omega_i##, v, and r} after the ith ball has struck it.
(b) The rotating assembly eventually assumes constant angular speed ##\omega^*##. Obtain ##\omega^*## in terms of v and r by solving the equation obtained in part (a). Argue how a constant ##\omega^*## does not violate energy conservation.
(c) Solve the expression obtained in part (a) to obtain ##\omega_i## in terms of {i, v, and r}.
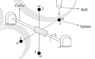
(d) If instead of a pair of spheres, we have two pairs of spheres as shown in figure below. What would be the new constant angular speed ##\omega^*## of the assembly (i.e. the answer corresponding to part (b)). (Attachment 2)
Homework Equations
The Attempt at a Solution
Let the rod be rotating with angular velocity ##\omega_i## before the next collision.
From conservation of angular momentum about centre of rod:
$$mvr+I\omega_i=I\omega_{i+1}+mv_1r$$
From conservation of energy:
$$\frac{1}{2}mv^2+\frac{1}{2}I\omega_i^2=\frac{1}{2}I\omega_{i+1}^2+ \frac{1}{2} mv_1^2$$
where I is the moment of inertia of rod+A+B and ##v_1## is the velocity of falling ball after collision.
Solving the two equations, I get:
$$\omega_{i+1}=\frac{7}{13}\omega_i+\frac{6v}{13r}$$
which is correct as per the answer key.
For part b, the question states that the angular velocity almost becomes constant.
Hence, ##\omega_{i+1}=\omega_{i}##. Using this, ##\omega^*=v/r##.
But what should I state for the argument? It looks odd to me that angular velocity becomes constant. The angular velocity should keep on increasing as the collisions take place.
Any help is appreciated. Thanks!
Attachments
Last edited: