Chuck 86
- 27
- 0
Homework Statement
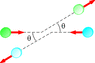
The mass of the blue (dark) puck in the figure below is 24.6% greater than the mass of the green (light) one.
Before colliding, the pucks approach each other with equal and opposite momenta, and the green puck has an initial speed of 12.0 m/s. The angle q = 33.5o. Calculate the speed of the blue puck after the collision if half the kinetic energy is lost during the collision.
Homework Equations
EFx=0=M(Green)V(green)cos(x)-M(blue)V(blue)Cos(x)
EFy=0=M(green)V(green)sin(x)-M(blue)V(blue)Sin(x)
( (1/2M(blue)V(blue)^2+M(green)V(green)^2)/2)=(1/2)M(green)V(green)^2+(1/2)M(blue)V(blue)^2
M(green)V'(green)=M(blue)V'(blue)
M(green)= (M(blue))/(2.46)
M(blue)= (2.46)M(green)
The Attempt at a Solution
I think these equations are correct but i don't knbow how I am going to get the mass of them. That would help a lot